D'Genauegkeet vun de geometreschen Parameteren vun de mechanesche Deeler gëtt beaflosst vu Dimensiounsfehler a Formfehler. Mechanesch Deel Designs spezifizéieren dacks Dimensiounstoleranzen a geometresch Toleranzen gläichzäiteg. Och wann et Differenzen a Verbindungen tëscht deenen zwee sinn, bestëmmen d'Genauegkeetsufuerderunge vu geometreschen Parameteren d'Relatioun tëscht geometrescher Toleranz an Dimensiounstoleranz, ofhängeg vun de Benotzungsbedingunge vum mechanesche Deel.
1. Verschidde Toleranzprinzipien iwwer d'Relatioun tëscht Dimensiounstoleranzen a geometreschen Toleranzen
Toleranzprinzipien si Reglementer déi bestëmmen ob dimensional Toleranzen a geometresch Toleranzen austauschbar benotzt kënne ginn oder net. Wann dës Toleranzen net aneneen ëmgewandelt kënne ginn, gi se als onofhängeg Prinzipien ugesinn. Op der anerer Säit, wann d'Konversioun erlaabt ass, ass et e verwandte Prinzip. Dës Prinzipien ginn weider an inklusiv Ufuerderunge klasséiert, maximal Entitéit Ufuerderunge, Minimum Entitéit Ufuerderunge, an reversibel Ufuerderunge.
2. Basis Terminologie
1) Lokal aktuell Gréisst D al, d al
D'Distanz gemooss tëscht zwee entspriechend Punkten op all normal Sektioun vun enger aktueller Fonktioun.
2) Extern Aktioun Gréisst D fe, d fe
Dës Definitioun bezitt sech op den Duerchmiesser oder d'Breet vun der gréisster idealer Uewerfläch, déi extern mat der aktueller bannenzeger Uewerfläch verbonnen ass oder déi klengst ideal Uewerfläch, déi extern mat der aktueller externer Uewerfläch op enger bestëmmter Längt vun der gemoosser Feature verbonnen ass. Fir assoziéiert Funktiounen muss d'Achs oder d'Mëttfläch vun der idealer Uewerfläch déi geometresch Bezéiung erhalen, déi vun der Zeechnung mam Datum gëtt.
3) In vivo Aktioun Gréisst D fi, d fi
Den Duerchmiesser oder d'Breet vun der klengster idealer Uewerfläch am Kierperkontakt mat der aktueller bannenzeger Uewerfläch oder der gréisster idealer Uewerfläch am Kierperkontakt mat der aktueller baussenzeger Uewerfläch bei enger bestëmmter Längt vun der Feature déi gemooss gëtt.
4) Maximal kierperlech effektiv Gréisst MMVS
Déi maximal kierperlech effektiv Gréisst bezitt sech op d'extern Effektgréisst am Staat wou et am meeschte kierperlech ass. Wann et ëm déi bannescht Uewerfläch geet, gëtt déi maximal effektiv Festgréisst berechent andeems de geometreschen Toleranzwäert (mat engem Symbol uginn) vun der maximaler Festgréisst subtrahéiert. Op der anerer Säit, fir déi baussenzeg Uewerfläch, gëtt déi maximal effektiv fest Gréisst berechent andeems de geometreschen Toleranzwäert (och mat engem Symbol uginn) op déi maximal fest Gréisst bäigefüügt.
MMVS = MMS ± T-Form
An der Formel ass déi baussenzeg Uewerfläch duerch e "+" Zeechen duergestallt, an déi bannescht Uewerfläch gëtt duerch e "-" Zeechen duergestallt.
5) Minimum kierperlech effikass Gréisst LMVS
Déi minimal effektiv Gréisst vun enger Entitéit bezitt sech op d'Gréisst vum Kierper wann et an engem minimalen effektive Staat ass. Wann Dir op déi bannescht Uewerfläch referéiert, gëtt déi minimal kierperlech effektiv Gréisst berechent andeems de geometreschen Toleranzwäert op déi minimal kierperlech Gréisst bäigefüügt gëtt (wéi mat engem Symbol an engem Bild uginn). Op der anerer Säit, wann Dir op déi baussenzeg Uewerfläch referéiert, gëtt déi minimal effektiv kierperlech Gréisst berechent andeems de geometreschen Toleranzwäert vun der minimaler kierperlecher Gréisst subtrahéiert (och mat engem Symbol an engem Bild uginn).
LMVS = LMS ±t-Form
An der Formel hëlt déi bannescht Uewerfläch den "+" Zeechen, an déi baussenzeg Uewerfläch hëlt d'"-" Zeechen.
3. Prinzip vun Onofhängegkeet
De Prinzip vun der Onofhängegkeet ass en Toleranzprinzip deen am Ingenieursdesign benotzt gëtt. Dëst bedeit datt déi geometresch Toleranz an Dimensiounstoleranz, déi an enger Zeechnung spezifizéiert sinn, getrennt sinn a keng Korrelatioun mateneen hunn. Béid Toleranzen mussen hir spezifesch Ufuerderungen onofhängeg erfëllen. Wann d'Form Toleranz an d'Dimensiounstoleranz de Prinzip vun der Onofhängegkeet befollegen, sollten hir numeresch Wäerter op der Zeechnung separat ouni zousätzlech Markéierung markéiert ginn.
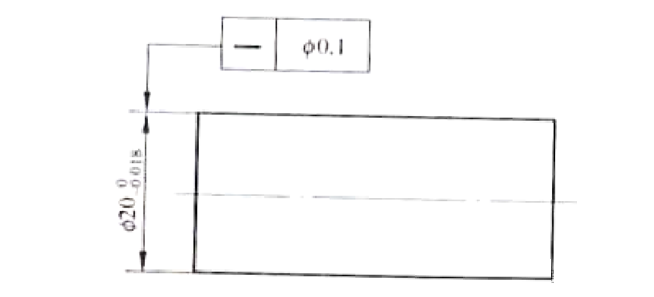
Fir d'Qualitéit vun den Deeler, déi an der Figur presentéiert ginn, ze garantéieren, ass et wichteg d'Dimensiounstoleranz vum Schaftduerchmiesser Ф20 -0,018 an d'Richtegkeet Toleranz vun der Achs Ф0,1 onofhängeg ze berücksichtegen. Dëst bedeit datt all Dimensioun den Designfuerderunge eleng muss entspriechen, an dofir sollten se separat iwwerpréift ginn.
D'Schacht Duerchmiesser soll tëscht dem Beräich vun Ф19,982 ze 20 falen, mat engem erlaabt straightness Feeler tëscht dem Beräich vun Ф0 ze 0,1. Obwuel de Maximum Wäert vun der Schacht Duerchmiesser eigentlech Gréisst kann op Ф20,1 verlängeren, et muss net kontrolléiert ginn. De Prinzip vun der Onofhängegkeet gëllt, dat heescht datt den Duerchmiesser keng ëmfaassend Inspektioun mécht.
4. Prinzip vun Toleranz
Wann e Symbol Bild schéngt no der Dimensioun Limite deviation oder Toleranz Zone Code vun engem eenzege Element op eng Zeechnen, et heescht, datt déi eenzeg Element Toleranz Ufuerderunge huet. Fir Inhaltsufuerderungen z'erreechen, muss déi aktuell Feature mat der maximaler kierperlecher Grenz entspriechen. An anere Wierder, déi extern handele Gréisst vun der Fonktioun däerf seng maximal kierperlech Grenz net iwwerschreiden, an déi lokal aktuell Gréisst däerf net méi kleng sinn wéi seng minimal kierperlech Gréisst.
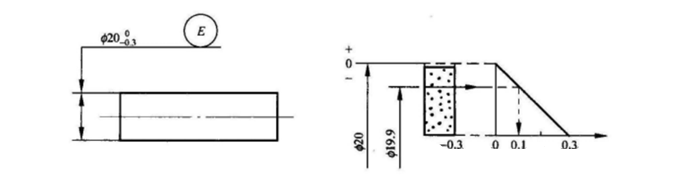
D'Figur weist datt de Wäert vun der dfe manner wéi oder gläich wéi 20mm soll sinn, während de Wäert vun dal méi grouss ass wéi oder gläich wéi 19.70mm. Wärend der Inspektioun gëtt d'zylindresch Uewerfläch als qualifizéiert ugesinn wann se duerch e vollforme Jauge mat engem Duerchmiesser vun 20mm passéiere kann a wann d'total lokal aktuell Gréisst gemooss op zwee Punkte méi wéi oder gläich wéi 19.70mm ass.
D'Toleranzfuerderung ass eng Toleranzfuerderung déi gläichzäiteg déi aktuell Gréisst a Formfehler am Dimensiounstoleranzberäich kontrolléiert.
5. Maximal Entitéit Ufuerderunge an hir Reversibilitéit Ufuerderunge
Op der Zeechnung, wann e Symbolbild den Toleranzwäert an der geometrescher Toleranzkëscht oder dem Referenzbréif follegt, heescht dat datt de gemoossene Element an d'Referenzelement déi maximal kierperlech Ufuerderunge adoptéieren. Ugeholl datt d'Bild nom Symbolbild nom geometreschen Toleranzwäert vum gemoossene Element markéiert ass. An deem Fall heescht et datt d'reversibel Ufuerderung fir déi maximal zolidd Ufuerderung benotzt gëtt.
1) Déi maximal Entitéitsfuerderung gëllt fir déi gemoossene Elementer
Wann Dir eng Feature moosst, wann e maximale Soliditéitsufuerderung applizéiert gëtt, gëtt de geometreschen Toleranzwäert vun der Feature nëmmen uginn wann d'Feature a senger maximaler zolitter Form ass. Wéi och ëmmer, wann d'tatsächlech Kontur vun der Feature vu sengem maximale festen Zoustand ofwäicht, dat heescht datt déi lokal aktuell Gréisst vun der maximaler massiver Gréisst anescht ass, kann d'Form an d'Positiounsfehlerwäert den Toleranzwäert iwwerschreiden, deen am maximalen festen Zoustand uginn ass, an de maximal iwwerschësseg Betrag wäert gläich op déi maximal zolidd Staat ginn. Et ass wichteg ze notéieren datt d'dimensional Toleranz vum gemoossene Element bannent senger maximaler a minimaler kierperlecher Gréisst sollt sinn, a seng lokal aktuell Gréisst däerf seng maximal kierperlech Gréisst net iwwerschreiden.
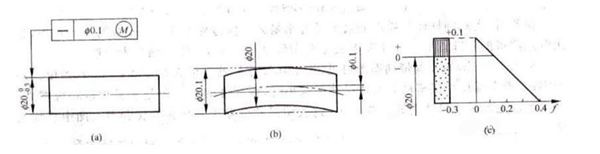
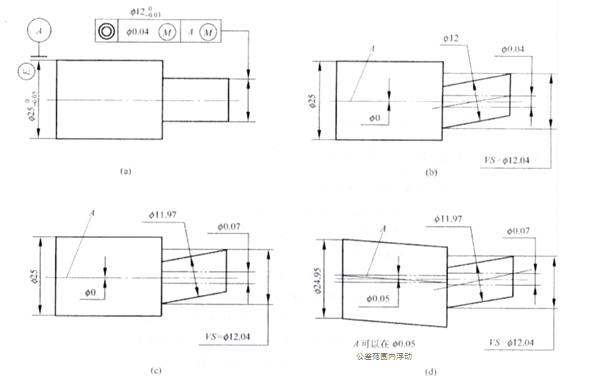
D'Figur illustréiert d'Richtegkeet Toleranz vun der Achs, déi un déi héchst kierperlech Ufuerderung hält. Wann de Schaft a sengem maximalen festen Zoustand ass, ass d'Richtegkeet Toleranz vu senger Achs Ф0,1 mm (Figur b). Wann d'tatsächlech Gréisst vum Schaft awer vu sengem maximale festen Zoustand ofwäit, kann den zulässlechen Richtegkeetsfehler f vu senger Achs deementspriechend erhéicht ginn. D'Toleranzzon Diagramm an der Figur C weist déi entspriechend Relatioun.
Den Duerchmiesser vum Schaft soll am Beräich vun Ф19.7mm bis Ф20mm sinn, mat enger maximaler Limit vun Ф20.1mm. Fir d'Qualitéit vum Schaft z'iwwerpréiwen, moosst als éischt seng zylindresch Kontur géint eng Positiounsmoossnam, déi mat der maximaler kierperlecher effektiver Grenzgréisst vun Ф20.1mm entsprécht. Benotzt dann déi zwee-Punkt-Methode fir déi lokal aktuell Gréisst vum Schaft ze moossen a sécherzestellen datt et an den akzeptablen kierperlechen Dimensiounen fällt. Wann d'Miessunge dëse Critèren entspriechen, kann de Schaft als qualifizéiert ugesi ginn.
Den dynamesche Diagramm vun der Toleranzzon illustréiert datt wann d'tatsächlech Gréisst vum maximalen festen Zoustand ëm Ф20 mm erofgeet, ass den zulässlechen Rechtheetsfehler f Wäert entspriechend erop. Wéi och ëmmer, déi maximal Erhéijung sollt d'Dimensiounstoleranz net iwwerschreiden. Dëst erméiglecht d'Transformatioun vun der Dimensiounstoleranz an d'Form a Positiounstoleranz.
2) Reversibel Ufuerderunge gi fir maximal Entitéit Ufuerderunge benotzt
Wann d'Ufuerderung fir Reversibilitéit op déi maximal Soliditéitsfuerderung applizéiert gëtt, muss déi aktuell Kontur vun der Feature, déi gemooss gëtt, mat senger maximaler Soliditéit effektiver Grenz konform sinn. Wann déi aktuell Gréisst vun der maximaler massiver Gréisst ofwäicht, ass de geometresche Feeler erlaabt de gegebene geometreschen Toleranzwäert ze iwwerschreiden. Zousätzlech, wann de geometreschen Fehler manner ass wéi de gegebene geometreschen Differenzwäert am maximale festen Zoustand, kann d'tatsächlech Gréisst och déi maximal zolidd-State Dimensiounen iwwerschreiden, awer de maximal zulässlechen Iwwerschoss ass eng Dimensiounsgemeinschaft fir déi fréier an eng bestëmmte geometresch Toleranz. fir déi lescht.
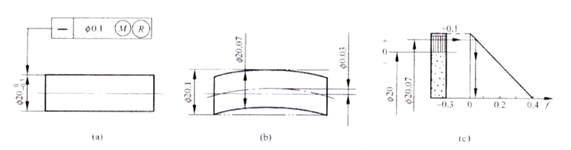
Figur A ass eng Illustratioun vun der Notzung vun reversiblen Ufuerderunge fir déi maximal fest Noutwendegkeete. D'Achs soll d fe ≤ Ф20,1 mm, Ф19,7 ≤ d al ≤ Ф20,1 mm erfëllen.
D'Formel hei ënnen erkläert datt wann d'tatsächlech Gréisst vun engem Schaft vum maximalen festen Zoustand op de minimale festen Zoustand ofwäicht, kann de Richtegkeetsfehler vun der Achs de maximale Wäert erreechen, deen d'Gläichheet Toleranzwäert vun 0,1 mm entsprécht an der Zeechnung plus. d'Gréisst Toleranz vum Schaft vun 0,3 mm. Dëst resultéiert am Ganzen Ф0,4 mm (wéi an der Figur c gewisen). Wann de Rechtheetsfehlerwäert vun der Achs manner ass wéi den Toleranzwäert vun 0,1 mm, deen op der Zeechnung uginn ass, ass et Ф0,03 mm, a seng aktuell Gréisst kann méi grouss sinn wéi déi maximal kierperlech Gréisst, an erreecht Ф20,07 mm (wéi an der Figur gewisen). b). Wann d'Richtegkeetsfehler null ass, kann seng aktuell Gréisst de maximale Wäert erreechen, wat seng maximal kierperlech effektiv Grenzgréisst vun Ф20.1mm entsprécht, sou datt d'Ufuerderung erfëllt fir geometresch Toleranz an Dimensiounstoleranz ze konvertéieren. Figur c ass eng dynamesch Diagramm datt d'Toleranz Zone vun der Relatioun uewen beschriwwen illustréiert.
Wärend der Inspektioun gëtt den aktuellen Duerchmiesser vum Schaft mat der ëmfaassender Positiounsmoossnam verglach, déi baséiert op der maximaler kierperlecher effektiver Grenzgréisst vun 20,1 mm entworf ass. Zousätzlech, wann d'tatsächlech Gréisst vun der Schaft, wéi gemooss mat der Zwee-Punkt-Methode, méi grouss ass wéi déi minimal kierperlech Gréisst vun 19,7 mm, da gëtt den Deel als qualifizéiert ugesinn.
3) Maximal Entitéit Ufuerderunge gëllen fir Datum Features
Wann Dir maximal Soliditéitsufuerderunge fir Datumfeatures applizéiert, muss den Datum un déi entspriechend Grenze konform sinn. Dëst bedeit datt wann d'extern Handlungsgréisst vun der Date Feature vun der entspriechender Grenzgréisst ënnerscheet, d'Datumelement erlaabt an engem bestëmmte Beräich ze bewegen. D'Schwemmberäich ass gläich wéi den Ënnerscheed tëscht der externer Handlungsgréisst vum Datumelement an der entspriechender Grenzgréisst. Wéi d'Datumelement vum Minimum Entitéitszoustand ofwäit, erhéicht säi schwiewend Beräich bis et de Maximum erreecht.
Figur A weist d'Koaxialitéit Toleranz vun der baussenzegen Kreesachs zu der baussenzeger Kreesachs. Déi gemoossene Elementer an Datumelementer adoptéieren déi maximal kierperlech Ufuerderunge zur selwechter Zäit.
Wann d'Element a sengem maximalen festen Zoustand ass, ass d'Koaxialitéit Toleranz vu senger Achs zum Datum A Ф0,04 mm, wéi an der Figur B. .
Wann e klengt Element gemooss gëtt, ass et zulässlech fir de Koaxialitéitsfehler vu senger Achs de maximale Wäert z'erreechen. Dëse Wäert ass gläich wéi d'Zomm vun zwou Toleranzen: d'Koaxialitéitstoleranz vun 0,04mm an der Zeechnung spezifizéiert an d'dimensional Toleranz vun der Achs, déi Ф0,07mm ass (wéi an der Figur c gewisen).
Wann d'Achs vum Datum op der maximaler kierperlecher Grenz ass, mat enger externer Gréisst vun Ф25mm, kann déi gegebene Koaxialitéitstoleranz op der Zeechnung Ф0,04mm sinn. Wann déi extern Gréisst vum Datum op déi minimal kierperlech Gréisst vun Ф24.95mm reduzéiert, kann d'Datumachs an der Dimensiounstoleranz vun Ф0.05mm schwammen. Wann d'Achs am extremen schwiewenden Zoustand ass, erhéicht d'Koaxialitéitstoleranz op den Datum Dimensiounstoleranzwäert vun Ф0,05 mm. Als Resultat, wann déi gemooss an Datum Elementer an der selwechter Zäit am minimale festen Zoustand sinn, kann de maximale Koaxialitéitsfehler bis zu Ф0.12mm erreechen (Figure d), wat d'Zomm vun 0.04mm fir Koaxialitéitstoleranz ass, 0.03mm fir Datum Dimensiounstoleranz an 0,05 mm fir Datum Achs Schwemm Toleranz.
6. Minimum Entitéit Ufuerderunge an hir Reversibilitéit Ufuerderunge
Wann Dir e Symbol Bild no der Toleranz Wäert oder Datum Bréif am geometreschen Toleranz Këscht op enger Zeechnung markéiert gesinn, et weist, datt de gemooss Element oder Datum Element muss de Minimum kierperlech Ufuerderunge treffen, respektiv. Op der anerer Säit, wann et e Symbol nom geometreschen Toleranzwäert vum gemoossene Element ass, heescht et datt d'reversibel Ufuerderung fir de Minimum Entityfuerderung benotzt gëtt.
1) Minimum Entitéit Ufuerderunge gëlle fir d'Ufuerderunge ënner dem Test
Wann Dir de Minimum Entitéitsfuerderung fir e gemoossene Element benotzt, däerf déi aktuell Kontur vum Element seng effektiv Grenz bei all bestëmmten Längt net iwwerschreiden. Zousätzlech soll déi lokal aktuell Gréisst vum Element net seng maximal oder minimal Entitéitsgréisst iwwerschreiden.
Wann d'Mindestfestfuerderung op eng gemoossene Feature applizéiert gëtt, gëtt de geometreschen Toleranzwäert uginn wann d'Feature am minimale festen Zoustand ass. Wéi och ëmmer, wann d'tatsächlech Kontur vun der Feature vu senger minimaler massiver Gréisst deviéiert, kann d'Form an d'Positiounsfehlerwäert den Toleranzwäert iwwerschreiden, deen am minimale festen Zoustand gëtt. An esou Fäll däerf d'aktiv Gréisst vun der gemoossene Feature seng minimal zolidd, effektiv Grenzgréisst net iwwerschreiden.
2) Reversibel Ufuerderunge gi fir Minimum Entitéit Ufuerderunge benotzt
Wann Dir d'reversibel Fuerderung op d'Mindestfestbedarf applizéiert, däerf déi gemoossene Fonktioun tatsächlech Kontur net seng minimal zolidd, effektiv Grenz bei all bestëmmten Längt iwwerschreiden. Zousätzlech soll seng lokal aktuell Gréisst net déi maximal zolidd Gréisst iwwerschreiden. Ënner dëse Bedéngungen ass net nëmmen de geometresche Feeler erlaabt de geometreschen Toleranzwäert ze iwwerschreiden, deen am minimale physeschen Zoustand uginn ass wann déi aktuell Gréisst vum gemoossene Element vun der minimaler kierperlecher Gréisst ofwäit, awer et ass och erlaabt déi minimal kierperlech Gréisst ze iwwerschreiden wann déi aktuell Gréisst ass anescht, virausgesat datt de geometresche Feeler méi kleng ass wéi de gegebene geometreschen Toleranzwäert.
Déicnc MaschinnUfuerderunge fir Minimum staark a seng reversibility soll nëmmen benotzt ginn, wann d'geometresch Toleranz benotzt gëtt der assoziéiert Zentrum Fonktioun ze kontrolléieren. Wéi och ëmmer, ob dës Ufuerderunge benotzen oder net hänkt vun de spezifesche Leeschtungsufuerderunge vum Element of.
Wann de gegebene geometreschen Toleranzwäert null ass, ginn déi maximal (Minimum) zolidd Ufuerderungen an hir reversibel Ufuerderunge als geometresch Null Toleranzen bezeechent. Zu dësem Zäitpunkt wäerten déi entspriechend Grenzen änneren, während aner Erklärungen onverännert bleiwen.
7. Bestëmmung vun geometreschen Toleranz Wäerter
1) Bestëmmung vun Sprëtz Form a Positioun Toleranz Wäerter
Am Allgemengen ass et recommandéiert datt Toleranzwäerter eng spezifesch Bezéiung verfollegen, mat Form Toleranz méi kleng wéi d'Positiounstoleranz an d'dimensional Toleranz. Wéi och ëmmer, et ass wichteg ze bemierken datt an ongewéinlechen Ëmstänn d'Richtegkeet Toleranz vun der Achs vum schlanke Schaft vill méi grouss ass wéi d'dimensional Toleranz. D'Positiounstoleranz soll d'selwecht sinn wéi d'dimensional Toleranz an ass dacks mat Symmetrietoleranzen vergläichbar.
Et ass wichteg ze garantéieren datt d'Positiounstoleranz ëmmer méi grouss ass wéi d'Orientéierungstoleranz. D'Positionéierungstoleranz kann d'Ufuerderunge vun der Orientéierungstoleranz enthalen, awer de Géigendeel ass net wouer.
Ausserdeem sollt déi ëmfaassend Toleranz méi grouss sinn wéi déi eenzel Toleranzen. Zum Beispill kann d'Zylindritéitstoleranz vun der Zylinderfläch méi grouss sinn wéi oder gläich wéi d'Richtegkeetstoleranz vun der Ronnheet, der Haaptlinn an der Achs. Ähnlech soll d'Flaachheetstoleranz vum Fliger méi grouss sinn wéi oder gläich wéi d'Richtegkeetstoleranz vum Fliger. Schlussendlech soll d'total Runout Toleranz méi grouss sinn wéi déi radial kreesfërmeg Runout, Ronnheet, Zylindrizitéit, Gläichheet vun der Haaptlinn an der Achs, an déi entspriechend Koaxialitéitstoleranz.
2) Bestëmmung vun onindicéierten geometreschen Toleranzwäerter
Fir d'Ingenieur Zeechnungen präzis a kloer ze maachen, ass et fakultativ fir d'geometresch Toleranz op den Zeechnungen unzeweisen fir d'geometresch Genauegkeet déi einfach ass ze garantéieren an der allgemenger Maschinnveraarbechtung. Fir Elementer deenen hir Form Toleranz Ufuerderunge net spezifesch op der Zeechnung uginn, ass d'Form a Positioun Genauegkeet och néideg. Weg kuckt op d'Ëmsetzung Reglementer vun GB / T 1184. Zeechnen Representatioune ouni Toleranz Wäerter soll am Titel Block Unhang oder an den techneschen Ufuerderunge an technesch Dokumenter notéiert ginn.
Héich Qualitéit Auto Ersatzdeeler,milling Deeler,an anStol-gedréint Deelerginn a China, Anebon gemaach. Produkter vun Anebon hunn ëmmer méi Unerkennung vun auslännesche Clienten kritt a laangfristeg a kooperativ Relatioune mat hinnen etabléiert. Anebon wäert de beschte Service fir all Client ubidden an häerzlech wëllkomm Frënn fir mat Anebon ze schaffen a géigesäitege Virdeeler zesummen ze etabléieren.
Post Zäit: Apr-16-2024