Přesnost geometrických parametrů mechanických součástí je ovlivněna jak rozměrovou chybou, tak chybou tvaru. Návrhy mechanických součástí často specifikují rozměrové tolerance a geometrické tolerance současně. Přestože mezi nimi existují rozdíly a souvislosti, požadavky na přesnost geometrických parametrů určují vztah mezi geometrickou tolerancí a rozměrovou tolerancí v závislosti na podmínkách použití mechanické části.
1. Několik tolerančních principů týkajících se vztahu mezi rozměrovými tolerancemi a geometrickými tolerancemi
Principy tolerance jsou předpisy, které určují, zda lze rozměrové tolerance a geometrické tolerance používat zaměnitelně či nikoli. Pokud tyto tolerance nelze vzájemně převést, jsou považovány za nezávislé principy. Na druhou stranu, pokud je konverze povolena, jde o související princip. Tyto principy se dále dělí na inkluzivní požadavky, maximální požadavky na entity, minimální požadavky na entity a vratné požadavky.
2. Základní terminologie
1) Místní skutečná velikost D al, d al
Vzdálenost měřená mezi dvěma odpovídajícími body na jakémkoli normálním úseku skutečného objektu.
2) Velikost vnějšího působení D fe, d fe
Tato definice se týká průměru nebo šířky největšího ideálního povrchu, který je externě spojen se skutečným vnitřním povrchem, nebo nejmenšího ideálního povrchu, který je externě připojen ke skutečnému vnějšímu povrchu při dané délce měřeného prvku. U přidružených prvků musí osa nebo středová rovina ideálního povrchu zachovat geometrický vztah daný výkresem a základnou.
3) Velikost působení in vivo Dfi, dfi
Průměr nebo šířka nejmenšího ideálního povrchu v kontaktu těla se skutečným vnitřním povrchem nebo největšího ideálního povrchu v kontaktu těla se skutečným vnějším povrchem při dané délce měřeného prvku.
4) Maximální fyzická efektivní velikost MMVS
Maximální fyzická efektivní velikost se týká velikosti vnějšího efektu ve stavu, kdy je fyzicky nejúčinnější. Pokud jde o vnitřní povrch, maximální efektivní velikost tělesa se vypočítá odečtením hodnoty geometrické tolerance (označené symbolem) od maximální velikosti tělesa. Na druhé straně pro vnější povrch se maximální efektivní velikost tělesa vypočítá přidáním hodnoty geometrické tolerance (také označené symbolem) k maximální velikosti tělesa.
MMVS = MMS± T-tvar
Ve vzorci je vnější povrch reprezentován znaménkem „+“ a vnitřní povrch je reprezentován znaménkem „-“.
5) Minimální fyzická efektivní velikost LMVS
Minimální efektivní velikost entity se vztahuje k velikosti těla, když je v minimálním efektivním stavu. Když se odkazuje na vnitřní povrch, minimální fyzická efektivní velikost se vypočítá přidáním hodnoty geometrické tolerance k minimální fyzické velikosti (jak je označeno symbolem na obrázku). Na druhé straně, když se odkazuje na vnější povrch, minimální efektivní fyzická velikost se vypočítá odečtením hodnoty geometrické tolerance od minimální fyzické velikosti (také označené symbolem na obrázku).
LMVS = LMS ± t-tvar
Ve vzorci má vnitřní povrch znaménko „+“ a vnější povrch má znaménko „-“.
3. Princip nezávislosti
Princip nezávislosti je toleranční princip používaný ve strojírenství. To znamená, že geometrická tolerance a rozměrová tolerance specifikovaná na výkrese jsou oddělené a nemají žádnou vzájemnou korelaci. Obě tolerance musí nezávisle splňovat své specifické požadavky. Pokud se tvarová a rozměrová tolerance řídí zásadou nezávislosti, měly by být jejich číselné hodnoty vyznačeny na výkrese samostatně bez dalšího značení.
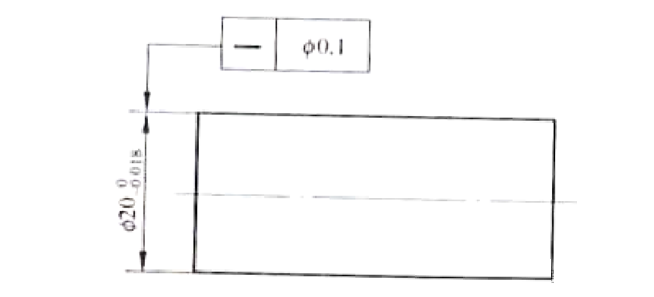
Aby byla zajištěna kvalita dílů uvedených na obrázku, je důležité nezávisle zvážit rozměrovou toleranci průměru hřídele Ф20 -0,018 a toleranci přímosti osy Ф0,1. To znamená, že každý rozměr musí splňovat konstrukční požadavky sám o sobě, a proto by měly být kontrolovány samostatně.
Průměr hřídele by měl spadat do rozsahu Ф19,982 až 20, s povolenou chybou přímosti v rozsahu Ф0 až 0,1. Přestože maximální hodnota skutečné velikosti průměru hřídele může dosahovat až 20,1, není nutné ji kontrolovat. Platí zásada nezávislosti, to znamená, že průměr nepodléhá komplexní kontrole.
4. Princip tolerance
Když se po rozměrové limitní odchylce nebo kódu toleranční zóny jednoho prvku na výkrese objeví obrázek symbolu, znamená to, že tento jednotlivý prvek má požadavky na toleranci. Aby byly splněny požadavky na omezení, musí skutečný prvek odpovídat maximální fyzické hranici. Jinými slovy, vnější působící velikost prvku nesmí překročit jeho maximální fyzickou hranici a místní skutečná velikost nesmí být menší než jeho minimální fyzická velikost.
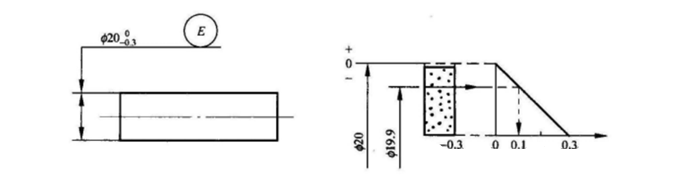
Obrázek ukazuje, že hodnota dfe by měla být menší nebo rovna 20 mm, zatímco hodnota dal by měla být větší nebo rovna 19,70 mm. Během inspekce bude válcový povrch považován za způsobilý, pokud může projít přes měřidlo plného tvaru o průměru 20 mm a pokud je celková místní skutečná velikost měřená ve dvou bodech větší nebo rovna 19,70 mm.
Požadavek na toleranci je požadavek na toleranci, který současně kontroluje skutečné chyby velikosti a tvaru v rozsahu tolerancí rozměrů.
5. Maximální požadavky na entity a požadavky na jejich vratnost
Když na výkrese následuje obrázek symbolu za hodnotou tolerance v rámečku geometrické tolerance nebo za referenčním písmenem, znamená to, že měřený prvek a referenční prvek splňují maximální fyzikální požadavky. Předpokládejme, že obrázek je označen za obrázkem symbolu za hodnotou geometrické tolerance měřeného prvku. V tomto případě to znamená, že pro maximální požadavek na pevné látky se použije reverzibilní požadavek.
1) Pro měřené prvky platí požadavek maximální entity
Pokud je při měření prvku uplatněn požadavek na maximální objem, hodnota geometrické tolerance prvku bude dána pouze tehdy, když je prvek ve svém maximálním plném tvaru. Pokud se však skutečný obrys prvku odchyluje od svého maximálního pevného stavu, což znamená, že místní skutečná velikost je odlišná od maximální velikosti pevného skupenství, hodnota chyby tvaru a polohy může překročit hodnotu tolerance udanou v maximálním pevném stavu a maximální přebytečné množství se bude rovnat maximálnímu pevnému skupenství. Je důležité si uvědomit, že rozměrová tolerance měřeného prvku by měla být v rámci jeho maximální a minimální fyzické velikosti a jeho místní skutečná velikost by neměla přesáhnout jeho maximální fyzickou velikost.
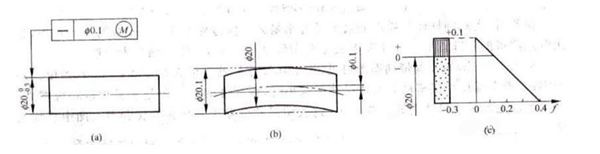
Obrázek znázorňuje toleranci přímosti osy, která splňuje nejvyšší fyzikální požadavky. Když je hřídel v maximálním pevném stavu, tolerance přímosti jeho osy je 0,1 mm (obrázek b). Pokud se však skutečná velikost hřídele odchýlí od jeho maximálního pevného stavu, může se přípustná chyba přímosti f jeho osy odpovídajícím způsobem zvýšit. Diagram toleranční zóny na obrázku C ukazuje odpovídající vztah.
Průměr hřídele by měl být v rozsahu Ф19,7 mm až Ф20 mm, s maximálním limitem Ф20,1 mm. Chcete-li zkontrolovat kvalitu hřídele, nejprve změřte jeho válcový obrys proti pozičnímu měřidlu, které odpovídá maximální fyzické efektivní hraniční velikosti 20,1 mm. Poté pomocí dvoubodové metody změřte místní skutečnou velikost hřídele a ujistěte se, že spadá do přijatelných fyzických rozměrů. Pokud měření splňují tato kritéria, lze hřídel považovat za způsobilý.
Dynamický diagram toleranční zóny ukazuje, že pokud se skutečná velikost zmenší z maximálního pevného stavu o Ф20 mm, přípustná chyba přímosti f se může odpovídajícím způsobem zvýšit. Maximální navýšení by však nemělo překročit rozměrovou toleranci. To umožňuje transformaci rozměrové tolerance na tvarovou a polohovou toleranci.
2) Reverzibilní požadavky se používají pro maximální požadavky na entity
Když je požadavek na vratnost aplikován na požadavek maximální pevnosti, musí skutečný obrys měřeného prvku odpovídat jeho efektivní hranici maximální pevnosti. Pokud se skutečná velikost odchyluje od maximální velikosti tělesa, může geometrická chyba překročit danou hodnotu geometrické tolerance. Navíc, pokud je geometrická chyba menší než daná hodnota geometrického rozdílu v maximálním pevném stavu, může skutečná velikost také překročit maximální rozměry pevného stavu, ale maximální přípustné překročení je rozměrovou shodou prvního a danou geometrickou tolerancí pro ty druhé.
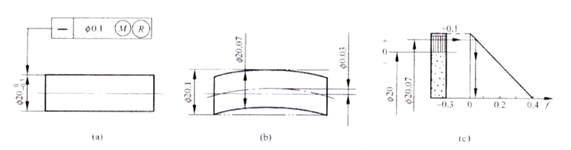
Obrázek A znázorňuje použití reverzibilních požadavků pro maximální požadavek na pevné látky. Osa by měla splňovat dfe ≤ Ф20,1 mm, Ф19,7 ≤ d al ≤ Ф20,1 mm.
Níže uvedený vzorec vysvětluje, že pokud se skutečná velikost hřídele odchyluje od maximálního pevného stavu k minimálnímu pevnému stavu, může chyba přímosti osy dosáhnout maximální hodnoty, která se rovná hodnotě tolerance přímosti 0,1 mm uvedené na výkrese plus tolerance velikosti hřídele 0,3 mm. Výsledkem je celkem 0,4 mm (jak je znázorněno na obrázku c). Je-li hodnota chyby přímosti osy menší než hodnota tolerance 0,1 mm uvedená na výkresu, je to 0,03 mm a její skutečná velikost může být větší než maximální fyzická velikost, dosahující 20,07 mm (jak je znázorněno na obrázku b). Když je chyba přímosti nulová, může jeho skutečná velikost dosáhnout maximální hodnoty, která se rovná jeho maximální fyzikální efektivní velikosti hranice Ф20,1 mm, čímž je splněn požadavek převodu geometrické tolerance na rozměrovou toleranci. Obrázek c je dynamický diagram, který znázorňuje toleranční pásmo výše popsaného vztahu.
Při kontrole je skutečný průměr hřídele porovnáván s komplexním polohovým měřidlem, které je navrženo na základě maximální fyzické efektivní mezní velikosti 20,1 mm. Navíc, pokud je skutečná velikost hřídele, měřená pomocí dvoubodové metody, větší než minimální fyzická velikost 19,7 mm, pak je díl považován za kvalifikovaný.
3) Maximální požadavky na entity se vztahují na základní prvky
Při aplikaci požadavků na maximální pevnost na prvky základny musí základ odpovídat odpovídajícím hranicím. To znamená, že když se velikost vnějšího působení pomocného prvku liší od jeho odpovídající hraniční velikosti, prvek základny se může pohybovat v určitém rozsahu. Plovoucí rozsah se rovná rozdílu mezi velikostí vnějšího působení pomocného prvku a odpovídající velikostí hranice. Jak se základní prvek odchyluje od stavu minimální entity, jeho plovoucí rozsah se zvyšuje, dokud nedosáhne maxima.
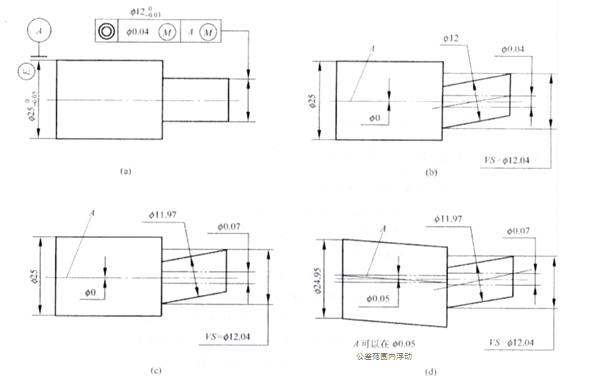
Obrázek A ukazuje toleranci souososti osy vnějšího kruhu k ose vnějšího kruhu. Měřené prvky a vztažné prvky současně splňují maximální fyzikální požadavky.
Když je prvek ve svém maximálním pevném stavu, tolerance souososti jeho osy k vztažnému bodu A je Ф0,04 mm, jak je znázorněno na obrázku B. Změřená osa by měla splňovat d fe≤Ф12,04 mm, Ф11,97≤d al≤Ф12 mm .
Když se měří malý prvek, je přípustné, aby chyba souososti jeho osy dosáhla maximální hodnoty. Tato hodnota se rovná součtu dvou tolerancí: tolerance souososti 0,04 mm specifikované na výkresu a rozměrové tolerance osy, která je Ф0,07 mm (jak je znázorněno na obrázku c).
Když je osa nulového bodu na maximální fyzické hranici, s vnější velikostí Ф25 mm, daná tolerance souososti na výkresu může být Ф0,04 mm. Pokud se vnější velikost základny zmenší na minimální fyzickou velikost Ф24,95 mm, může se pomocná osa pohybovat v rozměrové toleranci Ф0,05 mm. Když je osa v extrémním plovoucím stavu, tolerance souososti se zvýší na hodnotu tolerance rozměru základny 0,05 mm. Výsledkem je, že když jsou měřené a referenční prvky současně v minimálním pevném stavu, může maximální chyba souososti dosáhnout až 0,12 mm (obrázek d), což je součet 0,04 mm pro toleranci souososti, 0,03 mm. pro toleranci rozměrů základny a 0,05 mm pro toleranci plovoucí základny osy.
6. Minimální požadavky na entity a požadavky na jejich vratnost
Pokud vidíte obrázek symbolu označený za hodnotou tolerance nebo písmenem základny v poli geometrické tolerance na výkresu, znamená to, že měřený prvek nebo prvek základny musí splňovat minimální fyzikální požadavky. Na druhé straně, pokud je za hodnotou geometrické tolerance měřeného prvku symbol, znamená to, že pro požadavek minimální entity je použit reverzibilní požadavek.
1) Minimální požadavky na entity se vztahují na požadavky podle zkoušky
Při použití minimálního požadavku na entitu pro měřený prvek by skutečný obrys prvku neměl překročit jeho efektivní hranici při jakékoli dané délce. Místní skutečná velikost prvku by navíc neměla překročit jeho maximální nebo minimální velikost entity.
Pokud je na měřený prvek aplikován požadavek na minimální objem, je hodnota geometrické tolerance dána, když je prvek v minimálním pevném stavu. Pokud se však skutečný obrys prvku odchyluje od jeho minimální velikosti tělesa, hodnota chyby tvaru a polohy může překročit hodnotu tolerance danou minimálním tělesem. V takových případech by aktivní velikost měřeného prvku neměla překročit jeho minimální plnou, efektivní hraniční velikost.
2) Reverzibilní požadavky se používají pro minimální požadavky na entity
Při aplikaci reverzibilního požadavku na požadavek minimálního objemu by skutečný obrys měřeného prvku neměl překročit jeho minimální plnou, efektivní hranici při jakékoli dané délce. Jeho místní skutečná velikost by navíc neměla překročit maximální velikost tělesa. Za těchto podmínek je nejen dovoleno, aby geometrická chyba překročila hodnotu geometrické tolerance udanou v minimálním fyzickém stavu, když se skutečná velikost měřeného prvku odchyluje od minimální fyzické velikosti, ale je také povoleno překročit minimální fyzickou velikost, když skutečná velikost je jiná, pokud je geometrická chyba menší než daná hodnota geometrické tolerance.
Thecnc obráběnépožadavky na minimální objem a jeho reverzibilitu by se měly používat pouze tehdy, když se geometrická tolerance používá k ovládání souvisejícího středového prvku. To, zda tyto požadavky použít či nikoli, však závisí na konkrétních požadavcích na výkon prvku.
Když je daná hodnota geometrické tolerance nula, maximální (minimální) požadavky na tělesa a jejich vratné požadavky se označují jako nulové geometrické tolerance. V tomto okamžiku se odpovídající hranice změní, zatímco ostatní vysvětlení zůstanou nezměněna.
7. Stanovení hodnot geometrické tolerance
1) Stanovení tolerančních hodnot tvaru vstřiku a polohy
Obecně se doporučuje, aby hodnoty tolerance měly určitý vztah, přičemž tolerance tvaru je menší než tolerance polohy a tolerance rozměru. Je však důležité poznamenat, že za neobvyklých okolností může být tolerance přímosti osy štíhlého hřídele mnohem větší než rozměrová tolerance. Tolerance polohy by měla být stejná jako tolerance rozměrů a často je srovnatelná s tolerancemi symetrie.
Je důležité zajistit, aby tolerance polohy byla vždy větší než tolerance orientace. Tolerance polohy může zahrnovat požadavky tolerance orientace, ale opak není pravdou.
Kromě toho by celková tolerance měla být větší než individuální tolerance. Například tolerance válcovitosti povrchu válce může být větší nebo rovna toleranci přímosti zaoblení, základní čáry a osy. Podobně by tolerance rovinnosti roviny měla být větší nebo rovna toleranci přímosti roviny. A konečně, celková tolerance házení by měla být větší než radiální kruhové házení, kruhovitost, válcovitost, přímost primární čáry a osy a odpovídající tolerance souososti.
2) Stanovení neindikovaných hodnot geometrické tolerance
Aby byly technické výkresy stručné a jasné, je možné na výkresech uvést geometrickou toleranci pro geometrickou přesnost, kterou lze snadno zajistit při obecném zpracování obráběcích strojů. U prvků, jejichž požadavky na tvarovou toleranci nejsou na výkrese konkrétně uvedeny, je rovněž požadována tvarová a polohová přesnost. Viz prováděcí předpisy GB/T 1184. Vyobrazení výkresů bez tolerančních hodnot by mělo být uvedeno v příloze razítka nebo v technických požadavcích a technické dokumentaci.
Vysoce kvalitní autodíly,frézovací dílyaocelově soustružené dílyjsou vyrobeny v Číně, Anebon. Produkty Anebonu získávají stále větší uznání od zahraničních klientů a navazují s nimi dlouhodobé a kooperativní vztahy. Anebon bude poskytovat ty nejlepší služby pro každého zákazníka a upřímně vítá přátele, aby spolupracovali s Anebonem a společně vytvořili vzájemné výhody.
Čas odeslání: 16. dubna 2024