הדיוק של הפרמטרים הגיאומטריים של החלקים המכניים מושפע הן משגיאת מימד והן משגיאת צורה. עיצובי חלקים מכניים מציינים לעתים קרובות סובלנות ממדי וסובלנות גיאומטרית בו זמנית. למרות שיש הבדלים וקשרים בין השניים, דרישות הדיוק של פרמטרים גיאומטריים קובעות את הקשר בין סובלנות גיאומטרית וסובלנות מימדית, בהתאם לתנאי השימוש של החלק המכני.
1. מספר עקרונות סובלנות לגבי הקשר בין סובלנות ממדי וסובלנות גיאומטרית
עקרונות סובלנות הם תקנות שקובעות אם ניתן להשתמש בסובלנות ממדים ובסיבולות גיאומטריות לסירוגין או לא. אם לא ניתן להמיר סובלנות אלו זו בזו, הן נחשבות לעקרונות עצמאיים. מצד שני, אם מותר להמיר, זה עיקרון קשור. עקרונות אלה מסווגים עוד לדרישות כוללות, דרישות ישות מקסימליות, דרישות ישות מינימליות ודרישות הפיכות.
2. מינוח בסיסי
1) גודל מקומי מקומי D al, d al
המרחק שנמדד בין שתי נקודות מתאימות בכל קטע רגיל של תכונה ממשית.
2) פעולה חיצונית גודל D fe, d fe
הגדרה זו מתייחסת לקוטר או לרוחב של המשטח האידיאלי הגדול ביותר המחובר חיצונית למשטח הפנימי בפועל או למשטח האידיאלי הקטן ביותר המחובר חיצונית למשטח החיצוני בפועל באורך נתון של התכונה הנמדדת. עבור תכונות קשורות, הציר או המישור המרכזי של המשטח האידיאלי חייבים לשמור על היחס הגיאומטרי שניתן על ידי השרטוט עם הנתון.
3) פעולה In vivo גודל D fi, d fi
הקוטר או הרוחב של המשטח האידיאלי הקטן ביותר במגע הגוף עם המשטח הפנימי בפועל או המשטח האידיאלי הגדול ביותר במגע הגוף עם המשטח החיצוני בפועל באורך נתון של התכונה הנמדדת.
4) MMVS גודל פיזי יעיל מקסימלי
גודל האפקט הפיזי המקסימלי מתייחס לגודל ההשפעה החיצונית במצב שבו הוא הכי יעיל מבחינה פיזית. כאשר מדובר במשטח הפנימי, גודל המוצק האפקטיבי המרבי מחושב על ידי הפחתת ערך הסובלנות הגיאומטרית (מסומן בסמל) מגודל המוצק המרבי. מצד שני, עבור המשטח החיצוני, גודל המוצק המקסימלי האפקטיבי מחושב על ידי הוספת ערך הסובלנות הגיאומטרית (מסומן גם בסמל) לגודל המוצק המרבי.
MMVS= צורת MMS± T
בנוסחה, המשטח החיצוני מיוצג על ידי סימן "+", והמשטח הפנימי מיוצג על ידי סימן "-".
5) גודל מינימלי פיזי יעיל LMVS
הגודל האפקטיבי המינימלי של ישות מתייחס לגודל הגוף כאשר הוא נמצא במצב אפקטיבי מינימלי. כאשר מתייחסים למשטח הפנימי, הגודל האפקטיבי הפיזי המינימלי מחושב על ידי הוספת ערך הסובלנות הגיאומטרית לגודל הפיזי המינימלי (כפי שמצוין על ידי סמל בתמונה). מצד שני, כאשר מתייחסים למשטח החיצוני, הגודל הפיזי האפקטיבי המינימלי מחושב על ידי הפחתת ערך הסובלנות הגיאומטרית מהגודל הפיזי המינימלי (מסומן גם באמצעות סמל בתמונה).
LMVS= LMS ±t-shape
בנוסחה, המשטח הפנימי לוקח את הסימן "+", והמשטח החיצוני לוקח את הסימן "-".
3. עקרון העצמאות
עקרון העצמאות הוא עקרון סובלנות המשמש בתכנון הנדסי. משמעות הדבר היא שהסובלנות הגיאומטרית והסובלנות המימדית המצוינות בשרטוט נפרדות ואין להן מתאם זה עם זה. שני הסובלנות צריכים לעמוד בדרישות הספציפיות שלהם באופן עצמאי. אם סובלנות הצורה וסובלנות הממדים עוקבים אחר עקרון העצמאות, יש לסמן את הערכים המספריים שלהם על הציור בנפרד ללא כל סימונים נוספים.
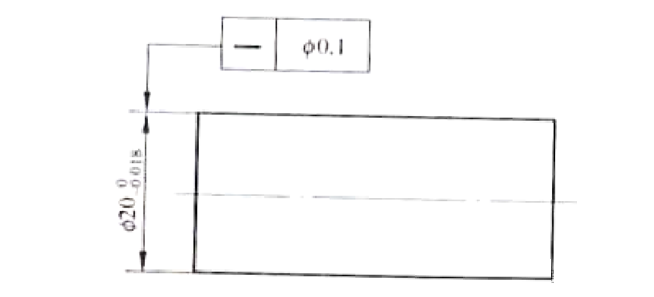
על מנת להבטיח את איכות החלקים המוצגים באיור, חשוב לקחת בחשבון את הסובלנות הממדית של קוטר הפיר Ф20 -0.018 ואת סובלנות הישר של הציר Ф0.1 באופן עצמאי. המשמעות היא שכל מימד חייב לעמוד בדרישות התכנון בפני עצמו, ולכן יש לבדוק אותן בנפרד.
קוטר הפיר צריך להיות בין הטווח של Ф19.982 עד 20, עם שגיאת ישרות מותרת בין הטווח של Ф0 עד 0.1. למרות שהערך המרבי של קוטר הפיר עשוי להגיע ל-Ф20.1, אין צורך לשלוט בו. עיקרון העצמאות חל, כלומר הקוטר אינו עובר בדיקה מקיפה.
4. עקרון הסובלנות
כשתמונת סמל מופיעה אחרי סטיית מגבלת הממד או קוד אזור סובלנות של אלמנט בודד בשרטוט, זה אומר שלאלמנט הבודד יש דרישות סובלנות. כדי לעמוד בדרישות הבלימה, התכונה בפועל חייבת לעמוד בגבול הפיזי המרבי. במילים אחרות, גודל הפעולה החיצוני של התכונה לא יעלה על הגבול הפיזי המרבי שלה, והגודל המקומי בפועל לא חייב להיות קטן מהגודל הפיזי המינימלי שלה.
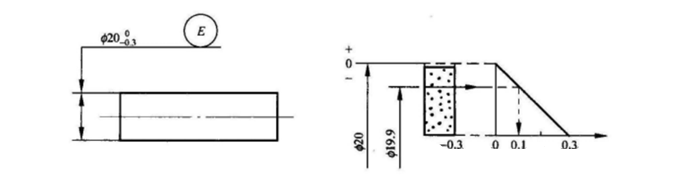
האיור מציין שהערך של dfe צריך להיות קטן או שווה ל-20 מ"מ, בעוד שהערך של dal צריך להיות גדול או שווה ל-19.70 מ"מ. במהלך הבדיקה, המשטח הגלילי ייחשב כשיר אם הוא יכול לעבור דרך מד צורה מלאה בקוטר של 20 מ"מ ואם סך הגודל המקומי בפועל שנמדד בשתי נקודות גדול או שווה ל-19.70 מ"מ.
דרישת הסובלנות היא דרישת סובלנות השולטת בו-זמנית על שגיאות הגודל והצורה בפועל בתוך טווח הסובלנות הממדית.
5. דרישות הישות המקסימליות ודרישות ההפיכות שלהן
בשרטוט, כאשר תמונת סמל עוקבת אחר ערך הסובלנות בתיבת הסובלנות הגיאומטרית או באות ההתייחסות, זה אומר שהאלמנט הנמדד ואלמנט הייחוס מאמצים את הדרישות הפיזיות המקסימליות. נניח שהתמונה מסומנת אחרי תמונת הסמל אחרי ערך הסובלנות הגיאומטרי של האלמנט הנמדד. במקרה זה, זה אומר שהדרישה ההפיכה משמשת עבור הדרישה המוצקה המקסימלית.
1) דרישת הישות המקסימלית חלה על האלמנטים הנמדדים
בעת מדידת תכונה, אם מיושמת דרישת מוצקות מרבית, ערך הסובלנות הגיאומטרית של התכונה יינתן רק כאשר התכונה נמצאת בצורתה המוצקה המקסימלית. עם זאת, אם קו המתאר בפועל של התכונה חורג מהמצב המוצק המרבי שלה, כלומר הגודל המקומי בפועל שונה מהגודל המוצק המרבי, ערך שגיאת הצורה והמיקום יכול לחרוג מערך הסובלנות שניתן במצב המוצק המרבי, וה הכמות העודפת המקסימלית תהיה שווה למצב המוצק המקסימלי. חשוב לציין שסובלנות הממדים של האלמנט הנמדד צריכה להיות בגודל הפיזי המקסימלי והמינימלי שלו, והגודל המקומי בפועל לא יעלה על הגודל הפיזי המרבי שלו.
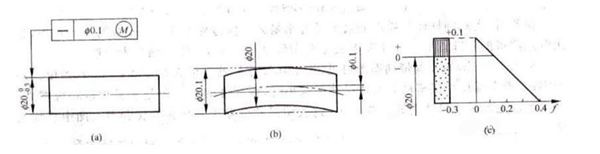
האיור ממחיש את סובלנות הישר של הציר, אשר עומד בדרישה הפיזית הגבוהה ביותר. כאשר הפיר נמצא במצב המוצק המרבי שלו, סובלנות הישר של הציר שלו היא Ф0.1 מ"מ (איור ב). עם זאת, אם הגודל האמיתי של הפיר חורג ממצבו המוצק המרבי, ניתן להגדיל את שגיאת הישר המותרת f של צירו בהתאם. דיאגרמת אזור הסובלנות המופיעה באיור C מציגה את הקשר המתאים.
קוטר הפיר צריך להיות בטווח של Ф19.7 מ"מ עד Ф20 מ"מ, עם מגבלה מקסימלית של Ф20.1 מ"מ. כדי לבדוק את איכות הפיר, מדוד תחילה את קווי המתאר הגלילי שלו מול מד מיקום התואם את גודל הגבול הפיזי האפקטיבי המרבי של Ф20.1 מ"מ. לאחר מכן, השתמש בשיטת שתי הנקודות כדי למדוד את הגודל המקומי בפועל של הפיר ולוודא שהוא נופל במידות הפיזיקליות המקובלות. אם המדידות עומדות בקריטריונים אלה, הפיר יכול להיחשב כשיר.
הדיאגרמה הדינמית של אזור הסובלנות ממחישה שאם הגודל בפועל יורד מהמצב המוצק המרבי ב-Ф20 מ"מ, ערך שגיאת הישר המותרת f מותר לגדול בהתאם. עם זאת, הגידול המרבי לא יעלה על סובלנות הממדים. זה מאפשר את הטרנספורמציה של הסובלנות הממדית לסובלנות הצורה והמיקום.
2) דרישות הפיכות משמשות לדרישות ישות מקסימליות
כאשר הדרישה להפיכות מיושמת על דרישת המוצקות המקסימלית, קו המתאר בפועל של התכונה הנמדדת חייב להתאים לגבול המוצק המקסימלי שלה. אם הגודל האמיתי חורג מגודל המוצק המרבי, השגיאה הגיאומטרית מותרת לחרוג מערך הסובלנות הגיאומטרית הנתון. בנוסף, אם השגיאה הגיאומטרית קטנה מערך ההפרש הגיאומטרי הנתון במצב המוצק המקסימלי, הגודל האמיתי יכול גם לחרוג מממדי המצב המוצק המרבי, אך העודף המרבי המותר הוא משותף ממדי לראשון וסובלנות גיאומטרית נתונה עבור האחרונים.
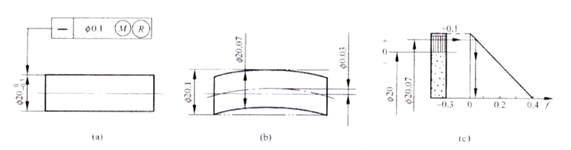
איור א' הוא המחשה של השימוש בדרישות הפיכות לדרישת המוצק המקסימלית. הציר צריך לעמוד ב-d fe ≤ Ф20.1 מ"מ, Ф19.7 ≤ d al ≤ Ф20.1 מ"מ.
הנוסחה שלהלן מסבירה שאם הגודל האמיתי של פיר חורג מהמצב המוצק המקסימלי למצב המוצק המינימלי, שגיאת הישר של הציר יכולה להגיע לערך המקסימלי, השווה לערך סובלנות הישר של 0.1 מ"מ שניתן בשרטוט פלוס סובלנות הגודל של הפיר של 0.3 מ"מ. התוצאה היא סך של Ф0.4 מ"מ (כמתואר באיור ג'). אם ערך שגיאת הישר של הציר קטן מערך הסובלנות של 0.1 מ"מ המופיע בשרטוט, הוא Ф0.03 מ"מ, וגודלו בפועל יכול להיות גדול מהגודל הפיזי המרבי, להגיע ל- Ф20.07 מ"מ (כמתואר באיור ב). כאשר שגיאת הישר היא אפס, הגודל האמיתי שלו יכול להגיע לערך המקסימלי, השווה לגודל הגבול הפיזי האפקטיבי המרבי שלו של Ф20.1 מ"מ, ובכך לענות על הדרישה של המרת סובלנות גיאומטרית לסובלנות מימדית. איור ג' הוא תרשים דינמי הממחיש את אזור הסובלנות של הקשר שתואר לעיל.
במהלך הבדיקה, קוטר הפיר בפועל מושווה למד המיקום המקיף, אשר תוכנן על בסיס גודל הגבול הפיזי האפקטיבי המרבי של 20.1 מ"מ. בנוסף, אם הגודל האמיתי של הפיר, כפי שנמדד בשיטת שתי הנקודות, גדול מהגודל הפיזי המינימלי של 19.7 מ"מ, אז החלק נחשב כשיר.
3) דרישות הישות המקסימליות חלות על מאפייני הנתונים
בעת החלת דרישות מוצקות מרבית על מאפייני דאטום, הנתון חייב להתאים לגבולות המתאימים. המשמעות היא שכאשר גודל הפעולה החיצוני של תכונת הדאטום שונה מגודל הגבול המתאים לו, אלמנט הדאטום רשאי לנוע בטווח מסוים. הטווח הצף שווה להפרש בין גודל הפעולה החיצוני של אלמנט הדאטום לגודל הגבול המתאים. כאשר אלמנט הדאטום סוטה ממצב הישות המינימלית, הטווח הצף שלו גדל עד שהוא מגיע למקסימום.
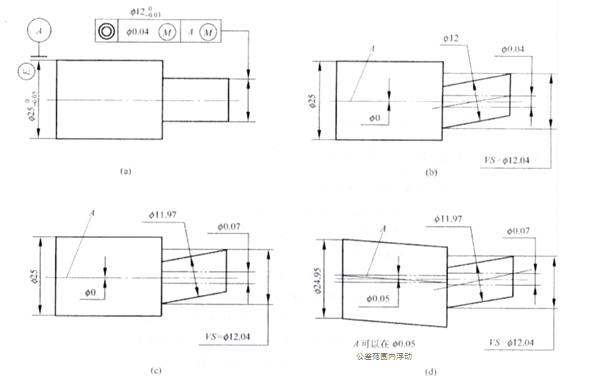
איור A מציג את סובלנות הקואקסיאליות של ציר המעגל החיצוני לציר המעגל החיצוני. האלמנטים הנמדדים ורכיבי הדאטום מאמצים את הדרישות הפיזיות המקסימליות בו-זמנית.
כאשר האלמנט נמצא במצב המוצק המקסימלי שלו, סובלנות הקואקסיאליות של הציר שלו לנתון A היא Ф0.04 מ"מ, כפי שמוצג באיור B. הציר הנמדד צריך לעמוד ב-d fe≤Ф12.04 מ"מ, Ф11.97≤d al≤Ф12 מ"מ .
כאשר אלמנט קטן נמדד, מותר ששגיאת הקואקסיאליות של הציר שלו תגיע לערך המקסימלי. ערך זה שווה לסכום של שתי סובלנות: סובלנות הקואקסיאליות של 0.04 מ"מ המצוינת בשרטוט והסובלנות הממדית של הציר, שהיא Ф0.07 מ"מ (כמתואר באיור ג').
כאשר ציר הנתון נמצא בגבול הפיזי המרבי, עם גודל חיצוני של Ф25 מ"מ, סובלנות הקואקסיאליות הנתונה בשרטוט יכולה להיות Ф0.04 מ"מ. אם הגודל החיצוני של הנתון מצטמצם לגודל הפיזי המינימלי של Ф24.95 מ"מ, ציר הנתון יכול לצוף בסובלנות הממדית של Ф0.05 מ"מ. כאשר הציר נמצא במצב צף קיצוני, סובלנות הקואקסיאליות עולה לערך הסובלנות הממדית של Ф0.05 מ"מ. כתוצאה מכך, כאשר האלמנטים הנמדדים והדאטום נמצאים במצב מוצק מינימלי בו-זמנית, שגיאת הקואקסיאליות המקסימלית יכולה להגיע עד Ф0.12 מ"מ (איור ד), שהוא הסכום של 0.04 מ"מ לסובלנות קואקסיאליות, 0.03 מ"מ. לסובלנות ממדית של נתון ו-0.05 מ"מ לסובלנות צפה של ציר הנתונים.
6. דרישות הישות המינימליות ודרישות ההפיכות שלהן
אם אתה רואה תמונת סמל המסומנת אחרי ערך הסובלנות או אות הדאטום בתיבת הסובלנות הגיאומטרית בשרטוט, זה מציין שהאלמנט הנמדד או אלמנט הדאטום חייבים לעמוד בדרישות הפיזיקליות המינימליות, בהתאמה. מצד שני, אם יש סמל אחרי ערך הסובלנות הגיאומטרי של האלמנט הנמדד, זה אומר שהדרישה ההפיכה משמשת לדרישת הישות המינימלית.
1) דרישות הישות המינימליות חלות על הדרישות במסגרת המבחן
בעת שימוש בדרישת הישות המינימלית עבור אלמנט נמדד, המתאר בפועל של האלמנט לא יעלה על הגבול האפקטיבי שלו בכל אורך נתון. בנוסף, הגודל המקומי בפועל של האלמנט לא יעלה על גודל הישות המקסימלי או המינימלי שלו.
אם דרישת המוצק המינימלית מוחלת על תכונה נמדדת, ערך הסובלנות הגיאומטרית ניתן כאשר התכונה נמצאת במצב מוצק מינימלי. עם זאת, אם קו המתאר בפועל של התכונה חורג מגודל המוצק המינימלי שלה, ערך שגיאת הצורה והמיקום יכול לחרוג מערך הסובלנות שניתן במצב המוצק המינימלי. במקרים כאלה, הגודל הפעיל של התכונה הנמדדת לא יעלה על גודל הגבול המוצק והיעיל המינימלי שלה.
2) דרישות הפיכות משמשות לדרישות מינימליות של ישות
בעת החלת הדרישה ההפיכה על דרישת המוצק המינימלית, המתאר בפועל של התכונה הנמדדת לא יעלה על הגבול המינימלי המוצק והיעיל שלו בכל אורך נתון. בנוסף, הגודל המקומי בפועל לא יעלה על הגודל המקסימלי המוצק. בתנאים אלה, לא רק שהשגיאה הגיאומטרית מותרת לחרוג מערך הסובלנות הגיאומטרית שניתן במצב הפיזי המינימלי כאשר הגודל האמיתי של האלמנט הנמדד חורג מהגודל הפיזי המינימלי, אלא מותר גם לחרוג מהגודל הפיזי המינימלי כאשר הגודל בפועל שונה, בתנאי שהשגיאה הגיאומטרית קטנה מערך הסובלנות הגיאומטרית הנתון.
הcnc מעובדיש להשתמש בדרישות למינימום מוצק והפיכות שלו רק כאשר משתמשים בסובלנות הגיאומטרית לשליטה בתכונה המרכזית הקשורה. עם זאת, האם להשתמש בדרישות אלו או לא תלוי בדרישות הביצועים הספציפיות של האלמנט.
כאשר ערך הסובלנות הגיאומטרית הנתון הוא אפס, הדרישות המקסימליות (המינימליות) המוצקות והדרישות ההפיכות שלהן מכונות סובלנות גיאומטריות אפס. בשלב זה, הגבולות המתאימים ישתנו בעוד הסברים אחרים יישארו ללא שינוי.
7. קביעת ערכי סובלנות גיאומטריים
1) קביעת ערכי סובלנות הזרקה וצורת ההזרקה
באופן כללי, מומלץ כי ערכי סובלנות יפעלו בהתאם לקשר ספציפי, כאשר סובלנות הצורה קטנה יותר מסובלת המיקום והסובלנות הממדית. עם זאת, חשוב לציין שבנסיבות חריגות, סובלנות הישר של ציר הציר הדק עשויה להיות גדולה בהרבה מהסובלנות המימדית. סובלנות המיקום צריכה להיות זהה לסובלנות הממדים ולעיתים קרובות ניתנת להשוואה לסובלנות סימטריה.
חשוב לוודא שסובלנות המיקום תהיה תמיד גדולה יותר מסובלת הכיוון. סובלנות המיקום עשויה לכלול את הדרישות של סובלנות ההתמצאות, אך ההיפך אינו נכון.
יתר על כן, הסובלנות המקיפה צריכה להיות גדולה יותר מהסובלנות האישית. לדוגמה, סובלנות הגליליות של משטח הגליל יכולה להיות גדולה או שווה לסובלנות הישר של העגלגלות, הקו הראשי והציר. באופן דומה, סובלנות השטיחות של המישור צריכה להיות גדולה או שווה לסבולת היישר של המישור. לבסוף, סובלנות היציאה הכוללת צריכה להיות גדולה יותר מהמסלול העגול הרדיאלי, העגלגלות, הגליליות, הישר של הקו והציר הראשי והסובלנות הקואקסיאלית המתאימה.
2) קביעת ערכי סובלנות גיאומטריים לא מסומנים
על מנת להפוך את השרטוטים ההנדסיים לתמציתיים וברורים, אופציונלי לציין את הסובלנות הגיאומטרית על השרטוטים לדיוק הגיאומטרי שקל להבטיח בעיבוד כלי מכונה כללי. עבור אלמנטים שדרישות סובלנות הצורה שלהם לא מצוינות במפורש בשרטוט, נדרש גם דיוק הצורה והמיקום. אנא עיין בתקנות היישום של GB/T 1184. יש לציין ייצוגי שרטוט ללא ערכי סובלנות בקובץ המצורף בלוק הכותרת או בדרישות הטכניות ובמסמכים הטכניים.
חלקי חילוף לרכב באיכות גבוהה,כרסום חלקים, וחלקים מסובבים מפלדהמיוצרים בסין, Anebon. מוצרי Anebon קיבלו יותר ויותר הכרה מלקוחות זרים ויצרו איתם קשרים ארוכי טווח ושיתוף פעולה. Anebon תספק את השירות הטוב ביותר עבור כל לקוח ותברך בכנות חברים לעבוד עם Anebon וליצור יתרונות הדדיים יחד.
זמן פרסום: 16 באפריל 2024