Mehaaniliste osade geomeetriliste parameetrite täpsust mõjutavad nii mõõtmete kui ka kuju viga. Mehaaniliste osade konstruktsioonid määravad sageli mõõtmete tolerantsid ja geomeetrilised tolerantsid üheaegselt. Kuigi nende kahe vahel on erinevusi ja seoseid, määravad geomeetriliste parameetrite täpsusnõuded geomeetrilise tolerantsi ja mõõtmete tolerantsi vahelise seose, olenevalt mehaanilise osa kasutustingimustest.
1. Mitu tolerantsi põhimõtet mõõtmete tolerantside ja geomeetriliste tolerantside vaheliste seoste kohta
Tolerantsi põhimõtted on eeskirjad, mis määravad, kas mõõtmete tolerantse ja geomeetrilisi tolerantse saab kasutada vaheldumisi või mitte. Kui neid tolerantse ei saa üksteiseks teisendada, peetakse neid iseseisvateks põhimõteteks. Teisest küljest, kui teisendamine on lubatud, on see seotud põhimõte. Need põhimõtted jagunevad täiendavalt kaasavateks nõueteks, üksuse maksimaalseteks nõueteks, olemi miinimumnõueteks ja pöörduvateks nõueteks.
2. Põhiterminoloogia
1) Kohalik tegelik suurus D al, d al
Kahe vastava punkti vahel mõõdetud kaugus tegeliku objekti mis tahes normaalsel lõigul.
2) Välise tegevuse suurus D fe, d fe
See määratlus viitab suurima ideaalse pinna läbimõõdule või laiusele, mis on väliselt ühendatud tegeliku sisepinnaga, või väikseimale ideaalsele pinnale, mis on väliselt ühendatud tegeliku välispinnaga mõõdetava tunnuse antud pikkuses. Seotud tunnuste puhul peab ideaalse pinna telg või kesktasand säilitama joonisel antud geomeetrilise suhte nullpunktiga.
3) In vivo toime suurus D fi, d fi
Väikseima ideaalse pinna läbimõõt või laius, mis on keha kokkupuutes tegeliku sisepinnaga või suurim ideaalne pind, mis puutub kokku keha tegeliku välispinnaga mõõdetava tunnuse antud pikkuses.
4) Maksimaalne füüsiline efektiivne suurus MMVS
Maksimaalne füüsiline efektiivne suurus viitab välise efekti suurusele seisundis, kus see on füüsiliselt kõige tõhusam. Sisepinna puhul arvutatakse maksimaalne efektiivne tahke suurus, lahutades geomeetrilise tolerantsi väärtuse (tähistatud sümboliga) maksimaalsest tahke suurusest. Teisest küljest arvutatakse välispinna puhul maksimaalne efektiivne tahke suurus, lisades maksimaalsele tahke suurusele geomeetrilise tolerantsi väärtuse (samuti tähistatud sümboliga).
MMVS= MMS± T-kuju
Valemis on välispind tähistatud märgiga "+" ja sisepind tähistatud märgiga "-".
5) Minimaalne füüsiline efektiivne suurus LMVS
Olemi minimaalne efektiivne suurus viitab keha suurusele, kui see on minimaalses efektiivses olekus. Sisepinnale viidates arvutatakse minimaalne füüsiline efektiivne suurus, lisades minimaalsele füüsilisele suurusele geomeetrilise tolerantsi väärtuse (nagu tähistab pildil olev sümbol). Seevastu välispinnale viidates arvutatakse minimaalne efektiivne füüsiline suurus, lahutades minimaalsest füüsilisest suurusest geomeetrilise tolerantsi väärtuse (seda tähistab ka pildil olev sümbol).
LMVS= LMS ±t-kuju
Valemis võtab sisepind märgi “+” ja välispind märgi “-”.
3. Sõltumatuse põhimõte
Sõltumatuse põhimõte on inseneriprojektis kasutatav tolerantsi põhimõte. See tähendab, et joonisel määratud geomeetriline tolerants ja mõõtmete tolerants on eraldiseisvad ja neil puudub korrelatsioon. Mõlemad tolerantsid peavad vastama oma spetsiifilistele nõuetele eraldi. Kui kujutolerants ja mõõtmete tolerants järgivad sõltumatuse põhimõtet, tuleks nende arvväärtused joonisele eraldi märkida ilma lisamärgistuseta.
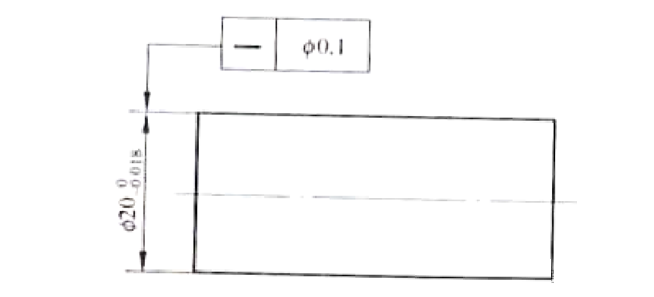
Joonisel kujutatud osade kvaliteedi tagamiseks on oluline arvestada võlli läbimõõdu Ф20 -0,018 mõõtmete tolerantsi ja telje sirguse tolerantsiga Ф0,1 sõltumatult. See tähendab, et iga mõõt peab iseseisvalt vastama projekteerimisnõuetele ja seetõttu tuleks neid eraldi kontrollida.
Võlli läbimõõt peaks jääma vahemikku Ф19,982 kuni 20, lubatud sirguse viga vahemikus Ф0 kuni 0,1. Kuigi võlli tegeliku läbimõõdu maksimaalne väärtus võib ulatuda Ф20,1-ni, ei pea seda kontrollima. Kehtib sõltumatuse põhimõte, mis tähendab, et läbimõõtu ei kontrollita põhjalikult.
4. Tolerantsuse põhimõte
Kui joonisel kuvatakse ühe elemendi mõõtmete piirhälbe või tolerantsi tsooni koodi järel sümbolpilt, tähendab see, et üksikule elemendile kehtivad tolerantsinõuded. Piiramisnõuete täitmiseks peab tegelik objekt vastama maksimaalsele füüsilisele piirile. Teisisõnu, objekti väline toimiv suurus ei tohi ületada selle maksimaalset füüsilist piiri ja kohalik tegelik suurus ei tohi olla väiksem selle minimaalsest füüsilisest suurusest.
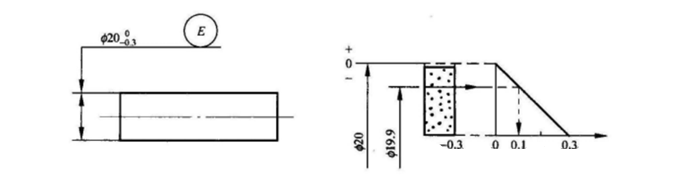
Joonis näitab, et dfe väärtus peaks olema väiksem või võrdne 20 mm, samas kui dal väärtus peaks olema suurem või võrdne 19,70 mm. Kontrollimise ajal loetakse silindriline pind kvalifitseerituks, kui see suudab läbida 20 mm läbimõõduga täiskujulist mõõturit ja kui kahes punktis mõõdetud kohalik tegelik kogumõõt on suurem või võrdne 19,70 mm.
Tolerantsi nõue on tolerantsi nõue, mis kontrollib samaaegselt tegelikke suurus- ja kujuvigu mõõtmete tolerantsi vahemikus.
5. Maksimaalsed üksuse nõuded ja nende pöörduvuse nõuded
Kui joonisel sümbolipilt järgib tolerantsi väärtust geomeetrilises hälbekastis või viitetähte, tähendab see, et mõõdetud element ja võrdluselement vastavad maksimaalsetele füüsikalistele nõuetele. Oletame, et pilt on märgistatud sümbolpildi järel pärast mõõdetud elemendi geomeetrilist tolerantsi väärtust. Sel juhul tähendab see, et maksimaalse tahke nõude jaoks kasutatakse pöörduvat nõuet.
1) Mõõdetavatele elementidele kehtib olemi maksimumnõue
Kui tunnuse mõõtmisel rakendatakse maksimaalse tugevuse nõuet, antakse tunnuse geomeetriline tolerantsi väärtus ainult siis, kui tunnus on maksimaalses täiskujus. Kui aga objekti tegelik kontuur erineb selle maksimaalsest tahkest olekust, mis tähendab, et kohalik tegelik suurus erineb maksimaalsest tahkes olekust, võib kuju ja asukoha vea väärtus ületada maksimaalses tahkes olekus antud tolerantsi väärtust ja maksimaalne ülejääk on võrdne maksimaalse tahke olekuga. Oluline on märkida, et mõõdetud elemendi mõõtmete tolerants peaks jääma selle maksimaalse ja minimaalse füüsilise suuruse piiresse ning selle kohalik tegelik suurus ei tohiks ületada maksimaalset füüsilist suurust.
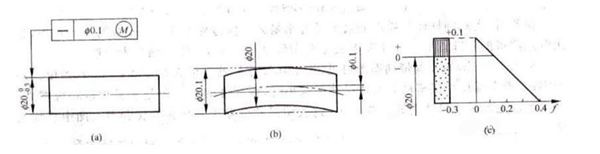
Joonis illustreerib telje sirguse tolerantsi, mis vastab kõrgeimatele füüsikalistele nõuetele. Kui võll on maksimaalses tahkes olekus, on selle telje sirguse tolerants Ф0,1 mm (joonis b). Kui aga võlli tegelik suurus erineb selle maksimaalsest tahkest olekust, saab selle telje lubatud sirgusviga f vastavalt suurendada. Joonisel C toodud tolerantsitsooni diagramm näitab vastavat seost.
Võlli läbimõõt peaks jääma vahemikku Ф19,7 mm kuni Ф20 mm, maksimaalselt Ф20,1 mm. Võlli kvaliteedi kontrollimiseks mõõtke esmalt selle silindriline piirjoon asendimõõturiga, mis vastab maksimaalsele füüsilisele efektiivsele piirde suurusele Ф20,1 mm. Seejärel kasutage kahepunktimeetodit, et mõõta võlli kohalikku tegelikku suurust ja tagada, et see jääks vastuvõetavate füüsiliste mõõtmete piiridesse. Kui mõõtmised vastavad neile kriteeriumidele, võib võlli lugeda kvalifitseerituks.
Tolerantsitsooni dünaamiline diagramm illustreerib, et kui tegelik suurus väheneb maksimaalsest tahkest olekust Ф20 mm, on lubatud sirguse vea f väärtus lubatud vastavalt suureneda. Maksimaalne kasv ei tohiks siiski ületada mõõtmete tolerantsi. See võimaldab muuta mõõtmete tolerantsi kuju ja asendi tolerantsiks.
2) Maksimaalsete oleminõuete jaoks kasutatakse pöörduvaid nõudeid
Kui pööratavuse nõuet rakendatakse maksimaalse tugevusnõude suhtes, peab mõõdetava tunnuse tegelik kontuur vastama selle maksimaalse terviklikkuse efektiivsele piirile. Kui tegelik suurus erineb maksimaalsest tahke suurusest, on geomeetriline viga lubatud ületada etteantud geomeetrilise tolerantsi väärtust. Lisaks, kui geomeetriline viga on väiksem kui antud geomeetrilise erinevuse väärtus maksimaalses tahkis olekus, võib tegelik suurus ületada ka maksimaalseid tahkismõõtmeid, kuid maksimaalne lubatud ülejääk on esimese ja antud geomeetrilise tolerantsi mõõtmete ühisosa. viimase jaoks.
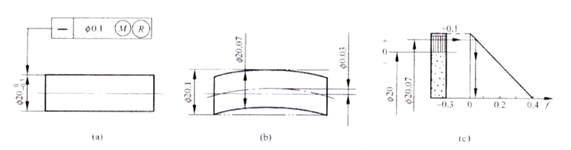
Joonis A on illustratsioon pöörduvate nõuete kasutamise kohta maksimaalse tahke nõude jaoks. Telg peaks rahuldama d fe ≤ Ф20,1 mm, Ф19,7 ≤ d al ≤ Ф20,1 mm.
Allolev valem selgitab, et kui võlli tegelik suurus erineb maksimaalsest tahkest olekust minimaalseks, võib telje sirguse viga jõuda maksimaalse väärtuseni, mis võrdub joonisel pluss sirguse tolerantsi väärtusega 0,1 mm. võlli suuruse tolerants 0,3 mm. Selle tulemuseks on kokku Ф0,4 mm (nagu on näidatud joonisel c). Kui telje sirguse vea väärtus on väiksem kui joonisel toodud tolerantsi väärtus 0,1 mm, on see Ф0,03 mm ja selle tegelik suurus võib olla suurem kui maksimaalne füüsiline suurus, ulatudes Ф20,07 mm-ni (nagu on näidatud joonisel b). Kui sirguse viga on null, võib selle tegelik suurus jõuda maksimaalse väärtuseni, mis võrdub selle maksimaalse füüsilise efektiivse piirisuurusega Ф20,1 mm, täites seega geomeetrilise tolerantsi mõõtmete tolerantsi teisendamise nõuded. Joonis c on dünaamiline diagramm, mis illustreerib ülalkirjeldatud seose tolerantsi tsooni.
Kontrollimisel võrreldakse võlli tegelikku läbimõõtu kõikehõlmava asendimõõturiga, mis on konstrueeritud lähtudes maksimaalsest füüsilisest efektiivsest piirde suurusest 20,1 mm. Lisaks, kui võlli tegelik suurus, mõõdetuna kahepunktimeetodil, on suurem kui minimaalne füüsiline suurus 19,7 mm, loetakse osa kvalifitseerituks.
3) Nullpunkti tunnustele kehtivad olemi maksimumnõuded
Nullpunkti omadustele maksimaalse tugevuse nõuete rakendamisel peab tugipunkt vastama vastavatele piiridele. See tähendab, et kui nullpunkti tunnuse välistegevuse suurus erineb selle vastavast piiri suurusest, on nullpunkti elemendil lubatud liikuda teatud vahemikus. Ujuv vahemik võrdub nullpunkti elemendi välistegevuse suuruse ja vastava piirde suuruse vahega. Kui nullpunkti element kaldub kõrvale minimaalse olemi olekust, suureneb selle ujuvvahemik kuni maksimumini.
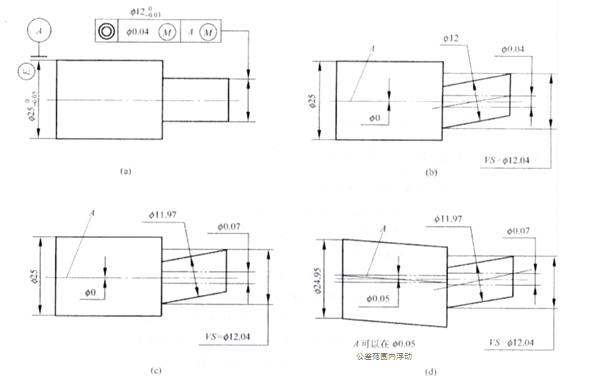
Joonisel A on näidatud ringjoone välistelje ja välisringi telje koaksiaalsustolerants. Mõõdetud elemendid ja nullelemendid vastavad maksimaalsetele füüsilistele nõuetele samal ajal.
Kui element on maksimaalses tahkes olekus, on selle telje koaksiaalsustolerants nullpunkti A suhtes Ф0,04 mm, nagu on näidatud joonisel B. Mõõdetud telg peaks vastama nõuetele d fe≤Ф12.04mm, Ф11.97≤d al≤Ф12mm .
Väikese elemendi mõõtmisel on lubatud, et selle telje koaksiaalsusviga jõuab maksimaalse väärtuseni. See väärtus võrdub kahe tolerantsi summaga: joonisel määratud koaksiaalsustolerants 0,04 mm ja telje mõõtmete tolerants, mis on Ф0,07 mm (nagu on näidatud joonisel c).
Kui nullpunkti telg on maksimaalsel füüsilisel piiril, välismõõduga Ф25mm, võib joonisel antud koaksiaalsustolerants olla Ф0,04mm. Kui nullpunkti väline suurus väheneb minimaalse füüsilise suuruseni Ф24,95 mm, võib nullpunkti telg hõljuda mõõtmete tolerantsi Ф0,05 mm piires. Kui telg on äärmises ujuvas olekus, suureneb koaksiaalsuse tolerants nullpunkti mõõtmete tolerantsi väärtuseni Ф0,05 mm. Selle tulemusel, kui mõõdetud ja nullelemendid on samaaegselt minimaalses tahkes olekus, võib maksimaalne koaksiaalsusviga ulatuda Ф0,12 mm-ni (joonis d), mis on 0,04 mm summa koaksiaalsustolerantsi puhul 0,03 mm. nullpunkti mõõtmete tolerantsi jaoks ja 0,05 mm tugipunkti telje ujuva tolerantsi jaoks.
6. Üksuse miinimumnõuded ja nende pöörduvuse nõuded
Kui näete joonisel geomeetrilise tolerantsi kastis pärast tolerantsi väärtust või nullpunkti tähte tähistatud sümbolipilti, siis näitab see, et mõõdetud element või nullpunkti element peab vastama vastavalt füüsilistele miinimumnõuetele. Teisest küljest, kui mõõdetava elemendi geomeetrilise tolerantsi väärtuse järel on sümbol, tähendab see, et olemi miinimumnõude jaoks kasutatakse pöörduvat nõuet.
1) Testitavatele nõuetele kehtivad üksuse miinimumnõuded
Mõõdetava elemendi minimaalse oleminõude kasutamisel ei tohiks elemendi tegelik piirjoon ühelgi antud pikkusel ületada selle tegelikku piiri. Lisaks ei tohiks elemendi kohalik tegelik suurus ületada selle maksimaalset ega minimaalset olemi suurust.
Kui mõõdetud objektile rakendatakse tahke miinimumnõuet, antakse geomeetriline tolerantsi väärtus, kui tunnus on minimaalses tahkes olekus. Kui aga tunnuse tegelik kontuur erineb selle minimaalsest tahke suurusest, võib kuju ja asukoha vea väärtus ületada minimaalses tahkes olekus antud tolerantsi väärtust. Sellistel juhtudel ei tohiks mõõdetud objekti aktiivne suurus ületada selle minimaalset tahket, efektiivset piiri suurust.
2) Olemi miinimumnõuete puhul kasutatakse pöörduvaid nõudeid
Pööratava nõude rakendamisel tahkete osakeste minimaalsele nõudele ei tohiks mõõdetud objekti tegelik piirjoon mingilgi pikkusel ületada selle minimaalset tahket efektiivset piiri. Lisaks ei tohiks selle kohalik tegelik suurus ületada maksimaalset tahke suurust. Nendel tingimustel ei tohi geomeetriline viga mitte ainult ületada minimaalses füüsikalises olekus antud geomeetrilist tolerantsi väärtust, kui mõõdetava elemendi tegelik suurus erineb minimaalsest füüsilisest suurusest, vaid on lubatud ületada ka minimaalset füüsilist suurust, kui tegelik suurus on erinev eeldusel, et geomeetriline viga on väiksem kui antud geomeetriline tolerantsi väärtus.
Thecnc töödeldudminimaalse tahke aine ja selle pööratavuse nõudeid tuleks kasutada ainult siis, kui geomeetrilist tolerantsi kasutatakse seotud keskosa juhtimiseks. Kuid see, kas neid nõudeid kasutada või mitte, sõltub elemendi konkreetsetest toimivusnõuetest.
Kui antud geomeetrilise tolerantsi väärtus on null, nimetatakse maksimaalseid (minimaalseid) tahkeid nõudeid ja nende pöörduvaid nõudeid geomeetrilisteks nulltolerantsideks. Siinkohal vastavad piirid muutuvad, samas kui muud seletused jäävad muutumatuks.
7. Geomeetriliste tolerantside väärtuste määramine
1) Sissepritse kuju ja asendi tolerantsi väärtuste määramine
Üldiselt on soovitatav, et tolerantsi väärtused järgiksid konkreetset seost, kusjuures kuju tolerants on väiksem kui asendi tolerants ja mõõtmete tolerants. Siiski on oluline märkida, et ebatavalistes olukordades võib sihvaka telje sirguse tolerants olla palju suurem kui mõõtmete tolerants. Asendi tolerants peaks olema sama mis mõõtmete tolerants ja on sageli võrreldav sümmeetria tolerantsiga.
Oluline on tagada, et positsioneerimise tolerants oleks alati suurem kui orientatsiooni tolerants. Positsioneerimise tolerants võib sisaldada orientatsiooni tolerantsi nõudeid, kuid vastupidine pole tõsi.
Lisaks peaks üldine tolerants olema suurem kui individuaalsed tolerantsid. Näiteks võib silindri pinna silindrilisuse tolerants olla suurem või võrdne ümaruse, algjoone ja telje sirguse tolerantsiga. Samamoodi peaks tasapinna tasasuse tolerants olema suurem või võrdne tasapinna sirguse tolerantsiga. Lõpuks peaks kogu väljajooksu tolerants olema suurem kui radiaalne ümmargune väljajooks, ümarus, silindrilisus, algjoone ja telje sirgus ning vastav koaksiaalsustolerants.
2) Näidata geomeetriliste tolerantsi väärtuste määramine
Tehniliste jooniste kokkuvõtlikuks ja arusaadavaks muutmiseks ei ole kohustuslik märkida joonistele geomeetriline tolerants geomeetrilise täpsuse jaoks, mida on lihtne tagada tööpinkide üldises töötlemises. Elementide puhul, mille vormitolerantsi nõudeid ei ole joonisel konkreetselt märgitud, nõutakse ka vormi ja asukoha täpsust. Tutvuge GB/T 1184 rakenduseeskirjadega. Tolerantside väärtusteta joonised tuleb märkida pealkirjaploki manuses või tehnilistes nõuetes ja tehnilistes dokumentides.
Kvaliteetsed autovaruosad,freesimise osadjaterasest treitud osadon valmistatud Hiinas, Anebonis. Aneboni tooted on pälvinud üha enam välisklientide tunnustust ning loonud nendega pikaajalisi ja koostöösuhteid. Anebon pakub igale kliendile parimat teenust ja tervitab siiralt sõpru Aneboniga koostööd tegema ja koos vastastikust kasu looma.
Postitusaeg: 16. aprill 2024