Kierre on kierre, joka leikataan työkappaleeseen joko ulkopuolelta tai sisältä ja jolla on useita tärkeitä tehtäviä. Ensinnäkin kierteet muodostavat mekaanisen liitoksen yhdistämällä sisäkierteitetyn tuotteen ulkokierteitettyyn tuotteeseen. Tällä liitännällä varmistetaan, että työkappaleen eri osat voidaan liittää tiukasti toisiinsa.
Lisäksi langoilla on tärkeä rooli liikkeen välittämisessä. Ne voivat muuntaa pyörivän liikkeen lineaariseksi liikkeeksi ja päinvastoin. Tämä ominaisuus on erityisen hyödyllinen monissa sovelluksissa, kuten koneissa, jotka vaativat lineaarista liikettä tiettyjen tehtävien suorittamiseen.
Lisäksi kierteet tarjoavat mekaanisia etuja. Kierteitä hyödyntämällä voidaan saavuttaa korkeampi mekaaninen suorituskyky kaikilta osin. Tämä sisältää lisääntyneen kuorman kantokyvyn, paremman löystymisen tai tärinänkestävyyden ja paremman voimansiirron tehokkuuden.
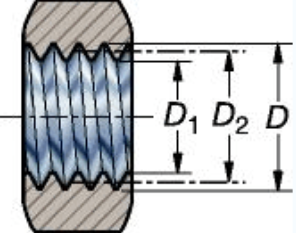
On olemassa erilaisia lankamuotoja, joista jokainen määrittää langan geometrian. Tärkeä näkökohta kierreprofiilissa on työkappaleen halkaisija. Tämä sisältää päähalkaisijan (kierteen suurin halkaisija) ja nousun halkaisijan (halkaisija kuvitteellisessa pisteessä, jossa kierteen leveys on nolla). Nämä mittaukset ovat tärkeitä sen varmistamiseksi, että kierteet sopivat kunnolla ja toimivat tehokkaasti.
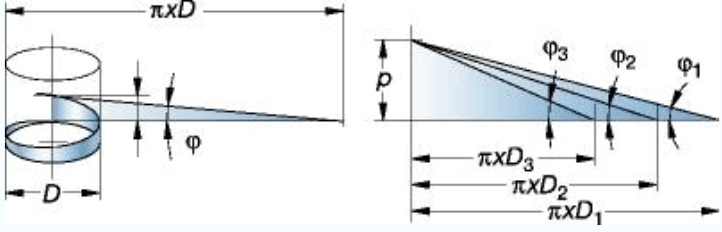
Säikeiden terminologian ymmärtäminen on ratkaisevan tärkeää säikeiden tehokkaan käytön kannalta. Joitakin keskeisiä termejä ovat johdin (aksiaalinen etäisyys, jonka kierre kulkee yhdessä täydellisessä kierrossa) ja nousu (etäisyys vierekkäisten kierteiden vastaavien pisteiden välillä). Tarkka johdon ja nousun mittaus on tärkeää tarkan kierteen suunnittelun ja yhteensopivuuden varmistamiseksi.
Yhteenvetona voidaan todeta, että säikeet palvelevat useita tärkeitä tehtäviä eri toimialoilla. Ne helpottavat mekaanisia liitoksia, välittävät liikettä ja tarjoavat mekaanisia etuja. Lankaprofiilien ja niihin liittyvän terminologian ymmärtäminen on ratkaisevan tärkeää säikeiden menestyksekkäälle käyttämiselle ja optimaalisen suorituskyvyn varmistamiseksi.
Pitch mysteerin ratkaiseminen: sen merkityksen ja laskentamenetelmän tutkiminen
Kierteen nousu on avaintekijä valmistuksen ja koneistuksen alalla. Sen merkityksen ymmärtäminen ja sen oikea laskeminen on erittäin tärkeää korkealaatuisten koneistettujen osien valmistuksessa. Tässä artikkelissa sukeltamme kierteen nousun monimutkaisuuteen, sen geometriaan ja kuinka se määritetään tarkasti. Lisäksi esittelemme Anebonin, prototyyppi-CNC-työstöpalveluihin ja asiakaskohtaiseen CNC-jyrsintään erikoistuneen yrityksen, joka tarjoaa nopeat ja luotettavat online-tarjoukset CNC-koneistukseen.
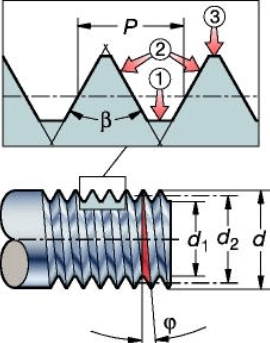
Kierteen geometria perustuu kierteen nousun halkaisijaan (d, D) ja nousuun (P): työkappaleen kierteen aksiaalinen etäisyys profiilin yhdestä pisteestä vastaavaan seuraavaan pisteeseen. Ajattele sitä kolmiona, joka kiertää työkappaletta. Tämä kolmion muotoinen rakenne määrää kierrekomponenttien tehokkuuden ja toimivuuden. Tarkka kierteen nousun laskenta on ratkaisevan tärkeää oikean sovituksen, optimaalisen kuorman jakautumisen ja koneistettujen osien tehokkaan suorituskyvyn varmistamiseksi.
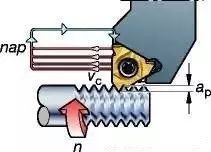
Valmistaja käyttää edistynyttä CNC-työstötekniikkaa sävelkorkeuden määrittämiseksi tarkasti. CNC-työstö tai tietokonenumeerinen ohjauskoneistus on valmistusprosessi, joka käyttää tietokoneohjattuja työstökoneita materiaalin poistamiseen tarkasti raaka-aineista koneistettujen osien muodostamiseksi. CNC-koneistuksen online-lainaus on monien ammattiyritysten tarjoama palvelu, jonka avulla asiakkaat voivat nopeasti ja helposti saada hinta-arvioita tilauksestaan.CNC-työstöosat.
Anebon on johtava rautakaupan yritys, joka on tarjonnut laadukkaita prototyyppi-CNC-työstöpalveluita ja räätälöityjä CNC-jyrsintää sen perustamisesta lähtien vuonna 2010. Anebon tarjoaa tehokkaita ja korkealaatuisia tuotteita ammattitaidolla ja huippuluokan laitteistolla. . Japanista tuotuja vakiokoneita. Niiden CNC-jyrsimet ja -sorvit sekä pintahiomakoneet mahdollistavat erinomaisen tuotteen tarkkuuden ja laadun. Lisäksi Anebonilla on ISO 9001:2015 -sertifikaatti, mikä osoittaa heidän sitoutumisensa korkeimpien tuotantostandardien ylläpitämiseen ja asiakastyytyväisyyteen.
Jakoväliä laskettaessa se ilmaistaan yleensä kierteinä tuumalla (TPI) tai millimetreinä. Metrinen kierteiden nousu on määritelty kahden vierekkäisen kierteen harjan väliseksi etäisyydeksi millimetreinä. Sitä vastoin tuumapohjaisissa kierrejärjestelmissä TPI tarkoittaa kierteitä lineaarista tuumaa kohti. Kierrevälin tarkka mittaaminen on ratkaisevan tärkeää kierreosien yhteensopivuuden varmistamiseksi ja mahdollisten ongelmien, kuten löysyyden, haurauden tai riittämättömän kuorman jakautumisen välttämiseksi.
CNC-työstösillä on tärkeä rooli tarkan sävelkorkeuden mittauksen saavuttamisessa. Hyödyntämällä uusinta teknologiaa ja tarkkuuslaitteita, CNC-koneistetut osat voivat täyttää tiukimmatkin vaatimukset ja spesifikaatiot. Kehittyneiden ohjelmistojen avulla CNC-koneet voivat suorittaa monimutkaisia kierrelaskelmia, mikä varmistaa oikean kierteen nousun jokaisessa ainutlaatuisessa sovelluksessa.
Yhteenvetona voidaan todeta, että nousun monimutkaisuuden ymmärtäminen ja sen tarkka laskeminen on erittäin tärkeää korkealaatuisten koneistettujen osien valmistuksessa. Hyödyntämällä prototyyppi-CNC-työstöpalveluita ja mukautettujaCNC-jyrsintä, valmistajat voivat saavuttaa tuotteissaan poikkeuksellista tarkkuutta ja laatua. Anebonin kaltaiset yritykset, jotka ovat sitoutuneet huippuosaamiseen ja uusimpien laitteiden kanssa, ovat edelläkävijöitä luotettavien ja tehokkaiden CNC-koneistuksen online-tarjouspalveluiden tarjoamisessa. Kierrevälin tarkan tietämyksen avulla valmistajat voivat luoda kierreosia, jotka täyttävät korkeimmat suorituskyky- ja toiminnallisuusstandardit.
1. 60° hammasmaisen ulkokierteen nousuhalkaisijan laskenta ja toleranssi (kansallinen standardi GB197/196)
a. Jaon halkaisijan peruskoon laskenta
Kierteen nousuhalkaisijan peruskoko = kierteen päähalkaisija – nousu × kertoimen arvo.
Kaavan esitys: d/DP × 0,6495
Esimerkki: Ulkokierteen M8-kierteen nousuhalkaisijan laskenta
8-1,25×0,6495=8-0,8119≈7,188
b. Yleisesti käytetty 6 tunnin ulkokierteen nousuhalkaisijan toleranssi (perustuu kierteen nousuun)
Yläraja on "0"
Alaraja on P0,8-0,095P1,00-0,112P1,25-0,118
P1,5-0,132P1,75-0,150P2,0-0,16
P2,5-0,17
Ylärajan laskentakaava on peruskoko ja alarajan laskentakaava d2-hes-Td2 on nousuhalkaisijan peruskoko-poikkeama-sallittu poikkeama.
M8:n 6h:n jakohalkaisijan toleranssiarvo: yläraja 7,188 alaraja: 7,188-0,118=7,07.
C. Yleisesti käytetty 6g-luokan ulkokierteen nousun halkaisijan peruspoikkeama: (perustuu kierteen nousuun)
P0,80-0,024P1,00-0,026P1,25-0,028P1,5-0,032
P1,75-0,034P2-0,038P2,5-0,042
Ylärajan laskentakaava d2-ges on peruskokopoikkeama
Alarajan laskentakaava d2-ges-Td2 on peruskokopoikkeamatoleranssi
Esimerkiksi M8:n 6 g:n jakohalkaisijan toleranssiarvo: ylempi raja-arvo 7,188-0,028=7,16 alaraja-arvo: 7,188-0,028-0,118=7,042.
Huomautus:
①Yllä mainitut kierteiden toleranssit perustuvat karkeisiin lankoihin ja myös hienojen lankojen toleranssit muuttuvat vastaavasti, mutta toleranssit ovat vain suurennettuja, joten ohjaus ei ylitä standardirajaa, joten niitä ei ole merkitty taulukkoon. Yläosa tuli ulos.
② Varsinaisessa tuotannossa kierrekäsittelylaitteiston suunnittelun vaatiman tarkkuuden ja puristusvoiman mukaan kierteitetyn kiillotetun tangon halkaisija kasvaa 0,04-0,08 verrattuna suunniteltuun kierteen halkaisijaan, joka on kierrekiillotetun kierteen halkaisija. sauva. Esimerkiksi yrityksemme M8-ulkokierteisen 6g kierrekiillotetun tangon halkaisija on 7,08-7,13, mikä on tällä alueella.
③Tuotantoprosessin tarpeet huomioon ottaen ulkokierteen nousuhalkaisijan alasäätöraja ilman lämpökäsittelyä ja pintakäsittelyä varsinaisessa tuotannossa tulisi pitää mahdollisimman pitkälle 6h tasolla.
2. 60° sisäkierteen nousuhalkaisijan laskenta ja toleranssi (GB197/196)
a.6H tason kierteen nousun halkaisijan toleranssi (perustuu kierteen nousuun)
yläraja:
P0,8+0,125P1,00+0,150P1,25+0,16P1,5+0,180
P1,25+0,00P2,0+0,212P2,5+0,224
Alempi raja-arvo on "0",
Ylärajan laskentakaava 2+TD2 on peruskoko + toleranssi.
Esimerkiksi sisäkierteen M8-6H nousuhalkaisija on: 7,188+0,160=7,348 yläraja: 7,188 on alaraja.
b. Sisäkierteen nousuhalkaisijan laskentakaava on sama kuin ulkokierteen
Eli D2 = DP × 0,6495, eli sisäkierteen nousuhalkaisija on yhtä suuri kuin nousuhalkaisija × kerroin arvo.
c.6G-luokan kierteen nousun halkaisijan peruspoikkeama E1 (perustuu kierteen nousuun)
P0,8+0,024P1,00+0,026P1,25+0,028P1,5+0,032
P1,75+0,034P1,00+0,026P2,5+0,042
Esimerkki: M86G sisäkierteen nousuhalkaisijan yläraja: 7,188+0,026+0,16=7,374
Alaraja: 7,188+0,026=7,214
Ylärajakaava 2+GE1+TD2 on nousuhalkaisijan+poikkeaman+toleranssin peruskoko
Alaraja-arvon kaava 2+GE1 on nousuhalkaisijan koko+poikkeama
3. Ulkokierteen päähalkaisijan laskenta ja toleranssi (GB197/196)
a. Ulkokierteen 6 tunnin päähalkaisijan yläraja
Eli kierteen halkaisijan arvoesimerkki M8 on φ8.00 ja ylärajan toleranssi on “0″.
b. Ulkokierteen päähalkaisijan alarajan toleranssi luokka 6h (kierteen nousun perusteella)
P0,8-0,15P1,00-0,18P1,25-0,212P1,5-0,236P1,75-0,265
P2,0-0,28P2,5-0,335
Päähalkaisijan alarajan laskentakaava: d-Td on kierteen päähalkaisijan perusmittatoleranssi.
Esimerkki: M8 ulkokierre 6h suuri halkaisija koko: yläraja on φ8, alaraja on φ8-0,212=φ7,788
c. Ulkokierteen päähalkaisijan 6g laskenta ja toleranssi
6 g ulkokierteen vertailupoikkeama (kierteen nousun perusteella)
P0,8-0,024P1,00-0,026P1,25-0,028P1,5-0,032P1,25-0,024P1,75-0,034
P2,0-0,038P2,5-0,042
Ylärajan laskentakaava d-ges on kierteen suuren halkaisijan vertailupoikkeaman perusmitta
Alarajan laskentakaava d-ges-Td on kierteen päähalkaisija-peruspoikkeama-toleranssin perusmitta
Esimerkki: M8 ulkokierre 6g luokan päähalkaisijan yläraja φ8-0,028=φ7,972.
Alaraja φ8-0,028-0,212=φ7,76
Huomautus: ①Kierteen päähalkaisija määräytyy kierrekiillotetun tangon halkaisijan ja kierteen vierintälevyn/rullan hammasprofiilin kulumisasteen mukaan, ja sen arvo on kääntäen verrannollinen kierteen ylä- ja keskihalkaisijaan. Saman aihion ja kierretyökalun perusteella mitä pienempi keskihalkaisija, sitä suurempi päähalkaisija, ja päinvastoin, mitä suurempi keskihalkaisija, sitä pienempi päähalkaisija.
② Lämpökäsittelyä ja pintakäsittelyä vaativien osien osalta, ottaen huomioon käsittelytekniikan ja todellisen tuotannon välisen suhteen, kierteen päähalkaisija on säädettävä luokan 6h alarajalla plus 0,04 mm tai enemmän. Esimerkiksi M8-ulkokierteellä hankauskierteen päähalkaisijan tulisi taata olevan yli 7,83 ja alle 7,95.
4. Sisäkierteen pienen halkaisijan laskenta ja toleranssi
a.Sisäkierteen pienen halkaisijan peruskoon laskeminen (D1)
Halkaisijaltaan pienen kierteen peruskoko = sisäkierteen peruskoko – nousu × kerroin
Esimerkki: Sisäkierteen M8 pienen halkaisijan peruskoko on 8-1,25×1,0825=6,646875≈6,647
b. Sisäkierteen 6H pienen halkaisijan toleranssin (kierteen nousun perusteella) ja pienen halkaisijan arvon laskenta
P0,8+0,2P1,0+0,236P1,25+0,265P1,5+0,3P1,75+0,335
P2,0+0,375P2,5+0,48
Luokan 6H sisäkierteen alarajapoikkeamakaava D1+HE1 on sisäkierteen peruskoko pieni halkaisija + poikkeama.
Huomautus: Bias-arvo on "0" 6H-tasolla
Laskentakaava sisäkierteen 6H tason ylärajalle = D1+HE1+TD1, eli sisäkierteen pienen halkaisijan peruskoko + poikkeama + toleranssi.
Esimerkki: 6H-luokan M8 sisäkierteen pienen halkaisijan yläraja on 6,647+0=6,647
6H-luokan M8 sisäkierteen pienen halkaisijan alaraja on 6,647+0+0,265=6,912
c.Sisäkierteen 6G pienen halkaisijan peruspoikkeaman (perustuen nousun) ja pienen halkaisijan arvon laskeminen
P0,8+0,024P1,0+0,026P1,25+0,028P1,5+0,032P1,75+0,034
P2.0+0.038P2.5+0.042
Laskentakaava sisäkierteen pienen halkaisijan alarajalle 6G = D1 + GE1 on sisäkierteen peruskoko + poikkeama.
Esimerkki: 6G-luokan M8 sisäkierteen pienen halkaisijan alaraja on 6,647+0,028=6,675
Kaava D1+GE1+TD1 6G-luokan M8 sisäkierteen pienen halkaisijan yläraja-arvolle on sisäkierteen peruskoko + poikkeama + toleranssi.
Esimerkki: 6G-luokan M8 sisäkierteen pienen halkaisijan yläraja on 6,647+0,028+0,265=6,94
Huomautus:
①Sisäkierteen hampaiden korkeus on suoraan verrannollinen sisäkierteen laakerimomenttiin, joten aihion tulee olla mahdollisimman pitkälle 6H-luokan ylärajan sisällä.
②Sisäkierteen koneistuksen aikana mitä pienempi sisäkierteen pieni halkaisija on, sitä pienempi työstötyökalun – kierteen – tehokkuus. Käytön kannalta katsottuna mitä pienempi pieni halkaisija, sitä parempi, mutta kattava harkinta, pientä halkaisijaa käytetään yleensä keskirajan ja ylärajan välillä, jos se on valurautaa tai alumiinia, sitä tulee käyttää pienen halkaisijan alaraja ja keskiraja .
③Kun sisäkierteen pieni halkaisija on 6G, se voidaan toteuttaa 6H:na. Tarkkuustaso ottaa huomioon pääasiassa kierteen nousuhalkaisijan pinnoitteen. Siksi vain hanan nousuhalkaisija otetaan huomioon kierteen käsittelyn aikana, eikä pientä halkaisijaa oteta huomioon. Valon reiän halkaisija.
5. Jakopään yhden jakomenetelmän laskentakaava
Yksijakolaskentakaava: n=40/Z
n: ympyröiden lukumäärä, joita jakopään tulee kääntää
Z: työkappaleen yhtä suuri osa
40: kiinteä indeksointipään numero
Esimerkki: Laskenta kuusikulmion jyrsimiseen
Korvaa kaava: n=40/6
Laskenta: ① Yksinkertaista murtoluvut: etsi pienin jakaja 2 ja jaa sillä, eli jaa osoittaja ja nimittäjä 2:lla yhtä aikaa, jolloin saadaan 20/3. Pisteitä pienennettynä sen tasajako pysyy samana.
② Murtolukujen laskenta: Tässä vaiheessa se riippuu osoittajan ja nimittäjän arvoista; jos osoittaja ja nimittäjä ovat suuria, laskenta suoritetaan.
20÷3=6(2/3) on n-arvo, eli jakopään tulee kääntyä 6(2/3) ympyrää. Tällä hetkellä murto-osasta on tullut murto-osa; desimaaliluvun 6 kokonaislukuosa on jakopään pitäisi kääntyä 6 täyttä ympyrää. Murto-osa 2/3 ja murto-osa voi olla vain 2/3 ympyrästä ja se on laskettava uudelleen tässä vaiheessa.
③Indeksointilevyn valinta ja laskenta: alle yhden ympyrän laskenta tulee toteuttaa indeksointipään indeksointilevyn avulla. Ensimmäinen vaihe laskennassa on samanaikaisesti laajentaa murto-osaa 2/3:lla. Esimerkiksi: jos pistemäärää suurennetaan 14 kertaa samaan aikaan, se on 28/42; jos se suurennetaan 10 kertaa samaan aikaan, pistemäärä on 20/30; jos se suurennetaan 13 kertaa samaan aikaan, pistemäärä on 26/39… Suurennetun asteikon tulee olla kellotaulun mukainen. Valitse reikien määrä siitä.
Tässä vaiheessa kannattaa kiinnittää huomiota:
①Valitun indeksointilevyn reikien lukumäärän on oltava jaollinen nimittäjällä 3. Esimerkiksi yllä olevassa esimerkissä 42 reikää on 14 kertaa 3, 30 reikää on 10 kertaa 3 ja 39 reikää 13 kertaa 3. .
② Murtolukujen laajennuksen on tapahduttava niin, että osoittaja ja nimittäjä laajenevat samanaikaisesti ja tasajako pysyy ennallaan, esim.
28/42=2/3×14=(2×14)/(3×14); 20/30=2/3×10=(2×10)/(3×10);
26/39=2/3×13=(2×13)/(3×13)
28/42 Nimittäjä 42 käyttää indeksointiin indeksinumeron 42 reikää; osoittaja 28 liikkuu eteenpäin ylemmän pyörän paikoitusreiässä ja kääntyy sitten 28-reiän yli, eli 29-reikä on nykyisen pyörän paikannusreikä, 20/30 on 10 reikää eteenpäin pyörän pyörimispaikassa. 30-reikäinen rekisterikilpi, ja 11. reikä on täsmälleen tämän pyörän sijoitusreikä. 26/39 on tämän pyörän kohdistusreikä 39-reikäisessä indeksilevyssä, ja 27:nnen reiän 26 reikää on käännetty eteenpäin.
Kuusikulmiota (kuudennesosaa) jyrsinnässä käytetään vaakoina reikiä, kuten 42 reikää, 30 reikää ja 39 reikää, jotka voivat olla jaettavissa kolmella: toiminto on käännä kahvaa 6 kertaa ja sitten siirrytään paikannusreiällä eteenpäin olla vastaavasti ylempi pyörä. Käänny taas 28+1/10+1/26+! Ylemmän 29/11/27 reiän reikää käytetään pyörän kohdistusreikänä.
Esimerkki 2: Laskelma 15-hampaisen hammaspyörän jyrsinnästä.
Korvaa kaava: n=40/15
Laske n=2(2/3)
Se on kääntää 2 täyttä ympyrää ja valita sitten indeksointireiät, jotka voivat olla jaettavissa kolmella, kuten 24, 30, 39, 42,51. Lisää 1 reikä, nimittäin 17, 21, 27, 29, 35, 37, 39, 45 reikää, tämän pyörän kohdistusrei'äksi.
Esimerkki 3: Indeksoinnin laskenta 82 hampaan jyrsinnässä.
Korvaa kaava: n=40/82
Laske n = 20/41
Eli niin kauan kuin on valittuna 41-reikäinen rekisterikilpi, käännä ylemmän pyörän kohdistusreikää 20+1, eli 21 reikää käytetään nykyisen pyörän kohdistusreikänä.
Esimerkki 4: Indeksoinnin laskenta 51 hampaan jyrsinnässä
Korvaa kaava n=40/51, koska pisteitä ei tällä hetkellä voi laskea, voit vain valita reiän suoraan, eli valita 51-reikäisen rekisterikilven ja kääntää sitten 51+1 yläpyörää sijoittelussa reikä, eli 52 reikää, kuten nykyinen pyörä. Sijoitusreiät esim.
Esimerkki 5: Indeksoinnin laskenta 100 hampaan jyrsinnässä.
Korvaa kaava n=40/100
Laske n = 4/10 = 12/30
Valitse 30-reikäinen rekisterikilpi ajoissa ja laita sitten 12+1 tai 13 reikää ylempään pyörän sijoitusreikään nykyiseksi pyörän paikannusreikään.
Jos kaikki indeksointikiekot eivät saavuta laskennassa tarvittavaa reikien määrää, laskennassa tulee käyttää yhdistelmäindeksimenetelmää, joka ei sisälly tähän laskentatapaan. Varsinaisessa tuotannossa käytetään yleensä hammaspyöriä, koska varsinainen toiminta yhdisteindeksilaskelman jälkeen on erittäin hankalaa.
6. Laskentakaava ympyrään piirretylle kuusikulmiolle
① Etsi ympyrän D kuusikulmion (S-pinnan) vastakkainen puoli
S = 0,866D on halkaisija × 0,866 (kerroin)
② Laske ympyrän halkaisija (D) kuusikulmion vastakkaiselta puolelta (S-pinta)
D = 1,1547S vastakkainen puoli × 1,1547 (kerroin)
7. Kuusikulman vastakkaisen sivun ja lävistäjäviivan laskentakaava kylmäsuuntaisessa prosessissa
① Etsi ulomman kuusikulmion vastakkaisen sivun (S) vastakkainen kulma e
e=1.13s Vastakkainen puoli×1.13
② Etsi vastakkainen kulma (e) sisemmän kuusikulmion vastakkaiselle puolelle (s).
e=1,14 s vastakkainen puoli × 1,14 (kerroin)
③ Selvitä diagonaalipään (D) materiaalihalkaisija ulkoisen kuusikulmion vastakkaisilta puolilta (s)
Ympyrän halkaisija (D) tulee laskea kuusikulmion vastakkaisen sivun (s-tason) mukaan (toinen kaava kohdassa 6), ja siirtymän keskiarvoa tulee suurentaa sopivasti, eli D≥1,1547s. Siirtymän määrää keskustasta voidaan vain arvioida.
8. Ympyrään piirretyn neliön laskentakaava
① Piirrä ympyrä (D) löytääksesi neliön vastakkaisen puolen (S-pinta)
S = 0,7071D on halkaisija × 0,7071
② Etsi ympyrä (D) neliön vastakkaiselta puolelta (S-pinta)
D = 1,414S vastakkainen puoli × 1,414
9. Laskentakaavat neliön vastakkaisille sivuille ja vastakkaisille kulmille kylmäsuuntausprosessissa
① Etsi vastakkainen kulma (e) ulkoneliön vastakkaiselle puolelle (S).
e=1.4s on vastakkaisen puolen (s)×1.4 parametri
② Etsi sisemmän neliön vastakkaisen sivun (s) vastakkainen kulma (e).
e=1.45s on vastakkaisen puolen (s)×1.45 kerroin
10. Kuusikulman tilavuuden laskentakaava
s20,866 × H/m/k tarkoittaa vastakkaista puolta × vastakkainen puoli × 0,866 × korkeus tai paksuus.
11. Katkaistun (kartion) tilavuuden laskentakaava
0,262H (D2 + d2 + D × d) on 0,262 × korkeus × (suuri pään halkaisija × suuri pään halkaisija + pieni pään halkaisija × pieni pään halkaisija + iso pään halkaisija × pieni pään halkaisija).
12. Pallon (kuten puoliympyrän muotoisen pään) tilavuuden laskentakaava
3,1416h2(Rh/3) on 3,1416×korkeus×korkeus×(säde–korkeus÷3).
13. Laskentakaava sisäkierretappien koneistusmitoille
1. Hanan päähalkaisijan D0 laskenta
D0=D+(0.866025P/8)×(0.5~1.3) on kierteen peruskoko, jonka halkaisija on suuri + 0.866025 jako 8×0.5~1.3.
Huomautus: Valinta 0,5–1,3 tulee määrittää sävelkorkeuden mukaan. Mitä suurempi äänenkorkeuden arvo, sitä pienempää kerrointa tulisi käyttää. Sitä vastoin mitä pienempi sävelkorkeusarvo on, sitä suurempi vastaavan kertoimen tulisi olla.
2. Kiertovälin halkaisijan laskeminen (D2)
D2=(3×0.866025P)/8, eli hanan halkaisija=3×0.866025×pitch÷8
3. Hanan halkaisijan laskeminen (D1)
D1=(5×0,866025P)/8 on hanan halkaisija=5×0,866025×pitch÷8
Neljätoista,
Materiaalin pituuden laskentakaava erimuotoisten kylmäpäiden muodostamiseen
Tunnetun ympyrän tilavuuskaava on halkaisija × halkaisija × 0,7854 × pituus tai säde × säde × 3,1416 × pituus. Eli d2 × 0,7854 × L tai R2 × 3,1416 × L
Laskettaessa vaaditun materiaalin tilavuus X÷halkaisija÷halkaisija÷0,7854 tai X÷säde÷3,1416 on materiaalin pituus.
Sarakekaava = X/(3.1416R2) tai X/0.7854d2
Kaavassa X edustaa vaaditun materiaalin tilavuusarvoa;
L edustaa todellisen ruokinnan pituusarvoa;
R/d edustaa todellista syöttösädettä tai halkaisijaa.
Anebonin tavoitteena on ymmärtää valmistuksen erinomaisia muodonmuutoksia ja tarjota huipputukea kotimaisille ja ulkomaisille asiakkaille koko sydämestäni vuodelle 2022 Korkealaatuinen ruostumaton teräs alumiini korkean tarkkuuden mittatilaustyönä valmistettu CNC-sorvausjyrsintäkoneistuksen varaosa ilmailualalle, laajentaaksemme kansainvälisiä markkinoitamme, Anebon toimittaa pääasiassa merentakaisille asiakkaillemme Huippulaadukkaita mekaanisia osia, jyrsittyjä osia ja cnc-sorvauspalvelua.
Kiinalainen tukkumyynti China Machinery Parts ja CNC-työstöpalvelu, Anebon tukee "innovoinnin, harmonian, ryhmätyön ja jakamisen, polkujen, käytännöllisen edistymisen henkeä". Anna meille mahdollisuus, niin aiomme todistaa kykymme. Ystävällisellä avullasi Anebon uskoo, että voimme luoda valoisan tulevaisuuden kanssasi yhdessä.
Postitusaika: 10.7.2023