Kaikille lanka on tuttu. Valmistavan teollisuuden kollegoina joudumme usein lisäämään lankoja asiakkaan tarpeiden mukaan käsitellessämme laitteistotarvikkeita, kutenCNC-työstöosat, CNC-sorvausosatjaCNC-jyrsintäosat.
1. Mikä lanka on?
Kierre on kierre, joka on leikattu työkappaleeseen joko ulkopuolelta tai sisältä. Lankojen päätoiminnot ovat:
1. Muodosta mekaaninen liitos yhdistämällä sisäkierretuotteita ja ulkokierretuotteita.
2. Siirrä liike muuntamalla pyörivä liike lineaariseksi liikkeeksi ja päinvastoin.
3. Hanki mekaanisia etuja.
2. Säikeen profiili ja terminologia
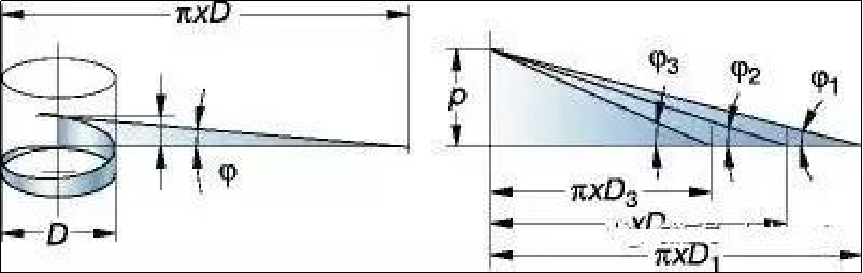
Kierreprofiili määrittää kierteen geometrian, mukaan lukien työkappaleen halkaisijan (pää-, nousu- ja sivuhalkaisijat); kierreprofiilikulma; nousu ja helix kulma.
1. Lankatermit
① Pohja: Pohjapinta, joka yhdistää kaksi vierekkäistä kierrekylkeä.
② kylki: kierteen sivupinta, joka yhdistää harjan ja hampaan pohjan.
③ Harja: yläpinta, joka yhdistää kaksi kylkiä.
P = nousu, mm tai kierteet tuumaa kohti (tpi)
ß = profiilikulma
ϕ = kierteen kierrekulma
d = ulkokierteen päähalkaisija
D = sisäkierteen suurin halkaisija
d1 = ulkokierteen pieni halkaisija
D1 = sisäkierteen pieni halkaisija
d2 = ulkokierteen nousuhalkaisija
D2 = kierteen sisähalkaisija
Jakohalkaisija, d2/D2
Tehokas langan halkaisija. Noin puolivälissä suuren ja pienen halkaisijan välillä.
Kierteen geometria perustuu kierteen nousun halkaisijaan (d, D) ja nousuun (P): työkappaleen kierteen aksiaalinen etäisyys profiilin yhdestä pisteestä vastaavaan seuraavaan pisteeseen. Tämä voidaan nähdä myös kolmiona, joka ohittaa työkappaleen.
vc = leikkausnopeus (m/min)
ap = kierteen kokonaissyvyys (mm)
nap = kierteen kokonaissyvyys (mm)
tpi = lankaa tuumaa kohti
Syöttö = pitch
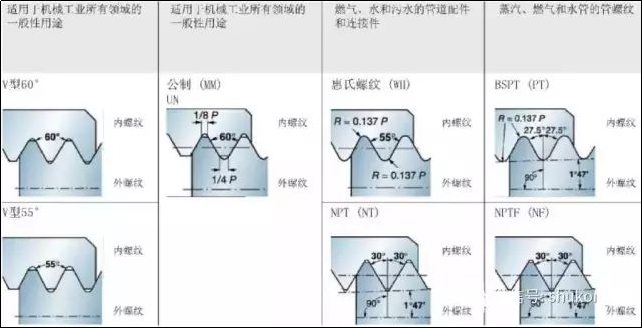
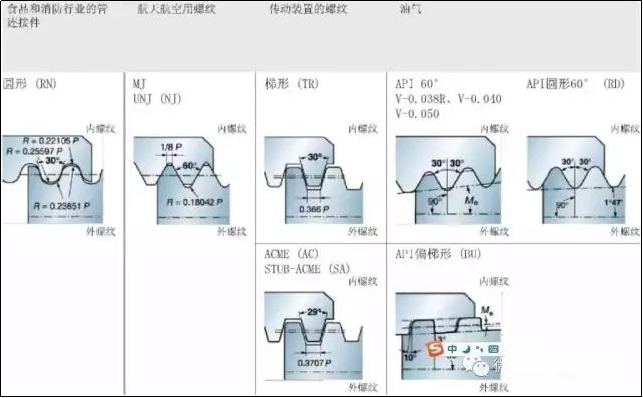
2. Tavallinen kierreprofiili
1. 60° hammastyypin ulkokierteen nousun halkaisijan laskeminen ja toleranssi (kansallinen standardi GB197/196)
a. Jaon halkaisijan peruskoon laskenta
Kierteen nousuhalkaisijan peruskoko = kierteen päähalkaisija – nousu × kertoimen arvo.
Kaavan esitys: d/DP × 0,6495
2. 60° sisäkierteen nousuhalkaisijan laskenta ja toleranssi (GB197/196)
a.6H tason kierteen nousun halkaisijan toleranssi (perustuu kierteen nousuun)
Yläraja:
P0,8+0,125P1,00+0,150P1,25+0,16P1,5+0,180
P1,25+0,00P2,0+0,212P2,5+0,224
Alempi raja-arvo on "0",
Ylärajan laskentakaava 2+TD2 on peruskoko + toleranssi.
Esimerkiksi sisäkierteen M8-6H nousuhalkaisija on: 7,188+0,160=7,348 Yläraja: 7,188 on alaraja.
b. Sisäkierteen nousuhalkaisijan laskentakaava on sama kuin ulkokierteen
Eli D2=DP×0,6495, eli sisäkierteen keskihalkaisija on yhtä suuri kuin kierteen nousu×kerroinarvon päähalkaisija.
c.6G-luokan kierteen nousun halkaisijan peruspoikkeama E1 (perustuu kierteen nousuun)
P0,8+0,024P1,00+0,026P1,25+0,028P1,5+0,032
P1,75+0,034P1,00+0,026P2,5+0,042
3. Ulkokierteen päähalkaisijan laskenta ja toleranssi (GB197/196)
a. Ulkokierteen 6 tunnin päähalkaisijan yläraja
Eli kierteen halkaisijan arvoesimerkki M8 on φ8.00 ja ylärajan toleranssi on “0″.
b. Ulkokierteen luokan 6h suurimman halkaisijan alarajan toleranssi (kierteen nousun perusteella)
P0,8-0,15P1,00-0,18P1,25-0,212P1,5-0,236P1,75-0,265
P2,0-0,28P2,5-0,335
Päähalkaisijan alarajan laskentakaava: d-Td on kierteen päähalkaisijan perusmitta – toleranssi.
4. Sisäkierteen pienen halkaisijan laskenta ja toleranssi
a. Sisäkierteen pienen halkaisijan peruskoon laskenta (D1)
Kierteen pienen halkaisijan peruskoko = sisäkierteen peruskoko – nousu × kerroin
5. Jakopään yhden jakomenetelmän laskentakaava
Yksijakomenetelmän laskentakaava: n=40/Z
n: kierrosten lukumäärä, jonka jakopään tulee kääntyä
Z: Työkappaleen yhtä suuri osa
40: kiinteä määrä jakopäätä
6. Ympyrään piirretyn kuusikulmion laskentakaava
① Etsi ympyrän D kuusikulmainen vastakkainen puoli (S-pinta).
S = 0,866D on halkaisija × 0,866 (kerroin)
② Laske ympyrän halkaisija (D) kuusikulmion vastakkaisilta puolilta (S-pinta)
D = 1,1547S on vastakkainen puoli × 1,1547 (kerroin)
7. Kuusikulmaisten vastakkaisten sivujen ja diagonaalien laskentakaava kylmäsuuntausprosessissa
① Etsi vastakkainen kulma e ulkoisen kuusikulmion vastakkaiselle puolelle (S).
e=1,13s on vastakkainen puoli × 1,13
②Etsi vastakkainen kulma (e) sisemmän kuusikulmion vastakkaiselle sivulle (s).
e=1,14s on vastakkainen puoli × 1,14 (kerroin)
③ Etsi vastakkaisen kulman (D) pään materiaalihalkaisija ulomman kuusikulmion vastakkaiselta puolelta (s)
Ympyrän halkaisija (D) tulee laskea (toinen kaava kohdassa 6) kuusikulmion vastakkaisen sivun (s pinnan) mukaisesti ja siirtymäkeskiarvoa tulee suurentaa sopivasti, eli D≥1,1547s. Siirtymäkeskuksen määrää voidaan vain arvioida.
8. Ympyrään piirretyn neliön laskentakaava
① Ympyrä (D) löytääksesi neliön vastakkaisen puolen (S-pinta)
S = 0,7071D on halkaisija × 0,7071
② Etsi ympyrä (D) neliön vastakkaisilta puolilta (S-pinta)
D = 1,414S on vastakkainen puoli × 1,414
9. Neliön vastakkaisten sivujen ja vastakkaisten kulmien laskentakaava kylmäsuuntaisessa prosessissa
① Etsi vastakkainen kulma (e) ulkoneliön vastakkaiselle puolelle (S).
e=1.4s on vastakkaisen puolen (s)×1.4 parametri
② Etsi vastakkainen kulma (e) sisemmän neliön vastakkaiselle sivulle (s).
e=1.45s on vastakkaisen puolen (s)×1.45 kerroin
10. Kaava kuusikulmion tilavuuden laskemiseksi
s20,866 × H/m/k tarkoittaa vastakkaista puolta × vastakkainen puoli × 0,866 × korkeus tai paksuus.
11. Katkaistun (kartion) kappaleen tilavuuden laskentakaava
0,262H (D2 + d2 + D × d) on 0,262 × korkeus × (iso pään halkaisija × iso pään halkaisija + pieni pään halkaisija × pieni pään halkaisija + iso pään halkaisija × pieni pään halkaisija).
12. Laskentakaava pallomaisen kappaleen (kuten puoliympyrän muotoisen pään) tilavuudelle
3,1416h2(Rh/3) on 3,1416×korkeus×korkeus×(säde–korkeus÷3).
13. Laskentakaava sisäkierteiden tappien koneistusmitoille
1. Hanan päähalkaisijan D0 laskenta
D0=D+(0.866025P/8)×(0.5~1.3) on kierteen peruskoko, jonka halkaisija on suuri + 0.866025 nousu ÷ 8×0.5 - 1.3.
Huomautus: Valinta 0,5 - 1,3 tulee vahvistaa sävelkorkeuden koon mukaan. Mitä suurempi äänenkorkeuden arvo, sitä pienempää kerrointa tulisi käyttää. Päinvastoin, mitä pienempi sävelkorkeus on, sitä vastaavaa suurempaa kerrointa tulisi käyttää.
2. Kiertovälin halkaisijan laskeminen (D2)
D2=(3×0.866025P)/8, eli hanan halkaisija=3×0.866025×pitch÷8
3. Hanan halkaisijan laskeminen (D1)
D1=(5×0,866025P)/8 on hanan halkaisija=5×0,866025×pitch÷8
14. Laskentakaava erimuotoiseen kylmäpäivystykseen käytettyjen materiaalien pituudelle
Tiedetään, että ympyrän tilavuuskaava on halkaisija × halkaisija × 0,7854 × pituus tai säde × säde × 3,1416 × pituus. Eli d2 × 0,7854 × L tai R2 × 3,1416 × L
Laskettaessa käsittelyyn tarvittavan materiaalin tilavuus X÷halkaisija÷halkaisija÷0,7854 tai X÷säde÷3,1416cnc-työstöosatjacnc-sorvausosaton materiaalin pituus.
Sarakekaava = X/(3.1416R2) tai X/0.7854d2
X kaavassa edustaa vaaditun materiaalin tilavuusarvoa;
L edustaa todellisen ruokinnan pituusarvoa;
R/d edustaa todellisen syötön sädettä tai halkaisijaa.
Postitusaika: 11.1.2023