Mekaanisten osien geometristen parametrien tarkkuuteen vaikuttavat sekä mitta- että muotovirhe. Mekaanisten osien suunnittelussa määritetään usein mittatoleranssit ja geometriset toleranssit samanaikaisesti. Vaikka näiden kahden välillä on eroja ja yhteyksiä, geometristen parametrien tarkkuusvaatimukset määräävät geometrisen toleranssin ja mittatoleranssin välisen suhteen mekaanisen osan käyttöolosuhteista riippuen.
1. Useita toleranssiperiaatteita mittatoleranssien ja geometristen toleranssien välisestä suhteesta
Toleranssiperiaatteet ovat määräyksiä, jotka määrittävät, voidaanko mittatoleransseja ja geometrisia toleransseja käyttää vaihtokelpoisesti vai ei. Jos näitä toleransseja ei voida muuntaa toisiksi, niitä pidetään itsenäisinä periaatteina. Toisaalta, jos muuntaminen on sallittua, se on siihen liittyvä periaate. Nämä periaatteet luokitellaan edelleen sisällyttäviin vaatimuksiin, kokonaisuuden enimmäisvaatimuksiin, kokonaisuuden vähimmäisvaatimuksiin ja palautuviin vaatimuksiin.
2. Perusterminologia
1) Paikallinen todellinen koko D al, d al
Kahden vastaavan pisteen välinen etäisyys mitattuna todellisen kohteen missä tahansa normaalissa osassa.
2) Ulkoinen toimintakoko D fe, d fe
Tämä määritelmä viittaa suurimman ideaalipinnan halkaisijaan tai leveyteen, joka on ulkoisesti liitetty todelliseen sisäpintaan, tai pienimpään ideaaliseen pintaan, joka on ulkoisesti liitetty todelliseen ulkopintaan mitattavan ominaisuuden tietyllä pituudella. Liitettyjen ominaisuuksien osalta ihanteellisen pinnan akselin tai keskitason on säilytettävä piirustuksen ja peruspisteen geometrinen suhde.
3) In vivo -toimintakoko D fi, d fi
Pienimmän ihanteellisen pinnan halkaisija tai leveys, joka on kosketuksessa varsinaiseen sisäpintaan, tai suurin ihanteellinen pinta, joka on kosketuksessa kehon todelliseen ulkopintaan mitattavan ominaisuuden tietyllä pituudella.
4) Suurin fyysinen tehollinen koko MMVS
Suurin fyysinen tehollinen koko viittaa ulkoisen efektin kokoon siinä tilassa, jossa se on fyysisesti tehokkain. Sisäpinnan osalta suurin tehollinen kokonaiskoko lasketaan vähentämällä geometrinen toleranssiarvo (merkitty symbolilla) suurimmasta kiintoainekoosta. Toisaalta ulkopinnalle suurin tehollinen kiintoainekoko lasketaan lisäämällä geometrinen toleranssiarvo (joka on myös merkitty symbolilla) enimmäismassan kokoon.
MMVS = MMS± T-muoto
Kaavassa ulkopintaa edustaa "+"-merkki ja sisäpintaa "-"-merkillä.
5) Pienin fyysinen tehollinen koko LMVS
Entiteetin pienin tehokas koko viittaa kehon kokoon sen ollessa minimitehotilassa. Kun viitataan sisäpintaan, fyysinen pienin tehollinen koko lasketaan lisäämällä geometrinen toleranssiarvo fyysiseen vähimmäiskokoon (kuten kuvassa oleva symboli osoittaa). Toisaalta, kun viitataan ulkopintaan, pienin efektiivinen fyysinen koko lasketaan vähentämällä geometrinen toleranssiarvo fyysisestä vähimmäiskoosta (joka on myös merkitty kuvassa olevalla symbolilla).
LMVS = LMS ±t-muoto
Kaavassa sisäpinta ottaa “+”-merkin ja ulkopinta “-”-merkin.
3. Riippumattomuuden periaate
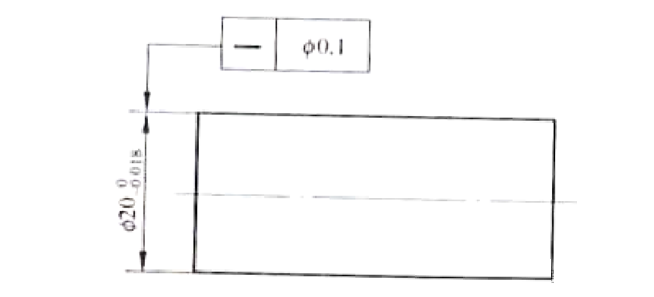
Riippumattomuusperiaate on suunnittelussa käytetty toleranssiperiaate. Tämä tarkoittaa, että piirustuksessa määritellyt geometrinen toleranssi ja mittatoleranssi ovat erillisiä eikä niillä ole korrelaatiota keskenään. Molempien toleranssien on täytettävä erityisvaatimukset itsenäisesti. Jos muototoleranssi ja mittatoleranssi noudattavat riippumattomuuden periaatetta, tulee niiden numeroarvot merkitä piirustukseen erikseen ilman lisämerkintöjä.
Kuvassa esitettyjen osien laadun varmistamiseksi on tärkeää huomioida akselin halkaisijan mittatoleranssi Ф20 -0,018 ja akselin suoruustoleranssi Ф0,1 erikseen. Tämä tarkoittaa, että jokaisen mitan on täytettävä suunnitteluvaatimukset yksinään, ja siksi ne on tarkastettava erikseen.
Akselin halkaisijan tulee olla välillä Ф19,982 - 20 ja sallitun suoruusvirheen välillä Ф0 - 0,1. Vaikka akselin halkaisijan todellisen koon maksimiarvo voi olla Ф20,1, sitä ei tarvitse säätää. Riippumattomuusperiaate pätee, eli halkaisijalle ei tehdä kattavaa tarkastusta.
4. Suvaitsevaisuuden periaate
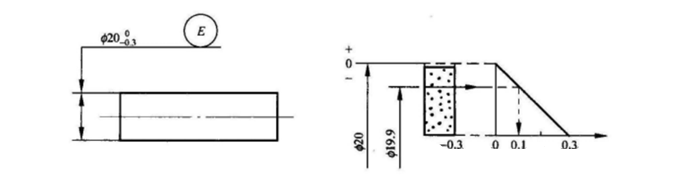
Kun piirustuksessa näkyy symbolikuva yksittäisen elementin mittarajapoikkeaman tai toleranssivyöhykekoodin jälkeen, se tarkoittaa, että yksittäisellä elementillä on toleranssivaatimukset. Suojausvaatimusten täyttämiseksi todellisen kohteen on oltava fyysisen enimmäisrajan mukainen. Toisin sanoen piirteen ulkoinen vaikuttava koko ei saa ylittää sen fyysistä enimmäisrajaa, eikä paikallinen todellinen koko saa olla pienempi kuin sen fyysinen vähimmäiskoko.
Kuva osoittaa, että dfe:n arvon tulee olla pienempi tai yhtä suuri kuin 20 mm, kun taas dal:n arvon tulee olla suurempi tai yhtä suuri kuin 19,70 mm. Tarkastuksen aikana lieriömäinen pinta katsotaan kelpuutetuksi, jos se läpäisee täysmuotoisen mittarin, jonka halkaisija on 20 mm ja jos kahdesta kohdasta mitattu paikallinen todellinen koko on suurempi tai yhtä suuri kuin 19,70 mm.
Toleranssivaatimus on toleranssivaatimus, joka ohjaa samanaikaisesti todellisia koko- ja muotovirheitä mittatoleranssialueella.
5. Kokonaisuuden enimmäisvaatimukset ja niiden palautusvaatimukset
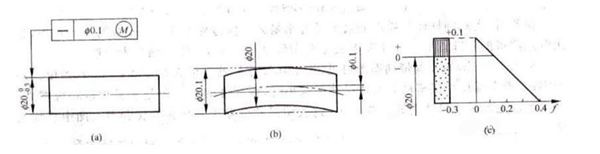
Piirustuksessa symbolikuva seuraa geometrisen toleranssilaatikon toleranssiarvoa tai viitekirjainta, mikä tarkoittaa, että mitattu elementti ja vertailuelementti täyttävät fyysiset maksimivaatimukset. Oletetaan, että kuva on merkitty symbolikuvan jälkeen mitatun elementin geometrisen toleranssiarvon jälkeen. Siinä tapauksessa se tarkoittaa, että reversiibeliä vaatimusta käytetään suurimmalle kiintoainetarpeelle.
1) Entiteettivaatimus koskee mitattuja elementtejä
Jos ominaisuutta mitattaessa sovelletaan maksimivahvuusvaatimusta, piirteen geometrinen toleranssiarvo annetaan vain, kun piirre on suurimmassa yhtenäisessä muodossaan. Jos ominaisuuden todellinen ääriviiva kuitenkin poikkeaa sen suurimmasta kiinteästä tilasta, mikä tarkoittaa, että paikallinen todellinen koko poikkeaa suurimmasta kiinteästä tilasta, muoto- ja sijaintivirhearvo voi ylittää suurimmassa kiinteässä tilassa annetun toleranssiarvon ja ylimääräinen enimmäismäärä on yhtä suuri kuin suurin sallittu kiinteä aine. On tärkeää huomata, että mitatun elementin mittatoleranssin tulee olla sen suurimman ja pienimmän fyysisen koon sisällä ja sen paikallinen todellinen koko ei saa ylittää sen fyysistä enimmäiskokoa.
Kuvassa on esitetty akselin suoruustoleranssi, joka noudattaa korkeinta fyysistä vaatimusta. Kun akseli on suurimmassa kiinteässä tilassaan, sen akselin suoruustoleranssi on Ф0,1mm (kuva b). Jos akselin todellinen koko kuitenkin poikkeaa sen suurimmasta kiinteästä tilasta, sen akselin sallittua suoruusvirhettä f voidaan kasvattaa vastaavasti. Kuvan C toleranssivyöhykekaavio esittää vastaavan suhteen.
Akselin halkaisijan tulee olla välillä Ф19.7mm - Ф20mm, enimmäisrajan Ф20.1mm. Tarkistaaksesi akselin laadun, mittaa ensin sen sylinterimäinen ääriviiva asentomittaria vasten, joka vastaa fyysistä maksimitehollista rajakokoa Ф20,1 mm. Käytä sitten kahden pisteen menetelmää akselin paikallisen todellisen koon mittaamiseen ja varmista, että se on hyväksyttävien fyysisten mittojen sisällä. Jos mitat täyttävät nämä kriteerit, akselia voidaan pitää kelvollisena.
Toleranssivyöhykkeen dynaaminen kaavio osoittaa, että jos todellinen koko pienenee suurimmasta kiinteästä olomuodosta Ф20 mm, sallitun suoruusvirheen f arvon annetaan kasvaa vastaavasti. Suurin lisäys ei kuitenkaan saa ylittää mittatoleranssia. Tämä mahdollistaa mittatoleranssin muuttamisen muoto- ja paikkatoleranssiksi.
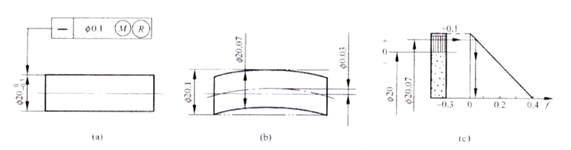
2) Käännettyjä vaatimuksia käytetään kokonaisuuden enimmäisvaatimuksiin
Kun käännettävyyden vaatimusta sovelletaan maksimivahvuusvaatimukseen, mitattavan piirteen todellisen ääriviivan on oltava sen maksimivahvuuden tehollisen rajan mukainen. Jos todellinen koko poikkeaa suurimmasta kiinteästä koosta, geometrinen virhe saa ylittää annetun geometrisen toleranssiarvon. Lisäksi, jos geometrinen virhe on pienempi kuin annettu geometrinen eroarvo suurimmassa solid-state-tilassa, todellinen koko voi myös ylittää suurimmat solid-state-mitat, mutta suurin sallittu ylitys on edellisen ja tietyn geometrisen toleranssin mittojen yhteisyys. jälkimmäiselle.
Kuvassa A on havainnollistettu käännettävien vaatimusten käyttöä kiintoaineen enimmäisvaatimuksen osalta. Akselin tulee täyttää d fe ≤ Ф20.1mm, Ф19.7 ≤ d al ≤ Ф20.1mm.
Alla oleva kaava selittää, että jos akselin todellinen koko poikkeaa suurimmasta kiinteästä tilasta minimiin, akselin suoruusvirhe voi saavuttaa maksimiarvon, joka on yhtä suuri kuin piirustuksessa annettu suoruustoleranssi 0,1 mm. akselin kokotoleranssi 0,3 mm. Tämä johtaa yhteensä Ф0,4 mm (kuten kuvassa c). Jos akselin suoruusvirhearvo on pienempi kuin piirustuksessa annettu toleranssiarvo 0,1 mm, se on Ф0,03 mm ja sen todellinen koko voi olla suurempi kuin suurin fyysinen koko saavuttaen 20,07 mm (kuten kuvassa näkyy). b). Kun suoruusvirhe on nolla, sen todellinen koko voi saavuttaa maksimiarvon, joka on yhtä suuri kuin sen suurin fyysinen tehollinen rajakoko Ф20,1 mm, mikä täyttää vaatimuksen geometrisen toleranssin muuntamisesta mittatoleranssiksi. Kuva c on dynaaminen kaavio, joka havainnollistaa edellä kuvatun suhteen toleranssialuetta.
Tarkastuksen aikana akselin todellista halkaisijaa verrataan kattavaan asentomittariin, joka on suunniteltu fyysisen maksimitehollisen rajakoon 20,1 mm perusteella. Lisäksi, jos akselin todellinen koko kaksipistemenetelmällä mitattuna on suurempi kuin fyysinen vähimmäiskoko 19,7 mm, osa katsotaan hyväksytyksi.
3) Entiteettivaatimukset koskevat perusominaisuuksia
Käytettäessä maksimivahvuusvaatimuksia perusominaisuuksiin, peruspisteen on noudatettava vastaavia rajoja. Tämä tarkoittaa, että kun peruspisteen ulkoisen toiminnan koko poikkeaa sen vastaavasta rajakoosta, peruspisteelementin sallitaan liikkua tietyllä alueella. Kelluva alue on yhtä suuri kuin peruselementin ulkoisen toiminnan koon ja vastaavan rajakoon välinen ero. Kun peruselementti poikkeaa minimikokonaisuuden tilasta, sen kelluva alue kasvaa, kunnes se saavuttaa maksimin.
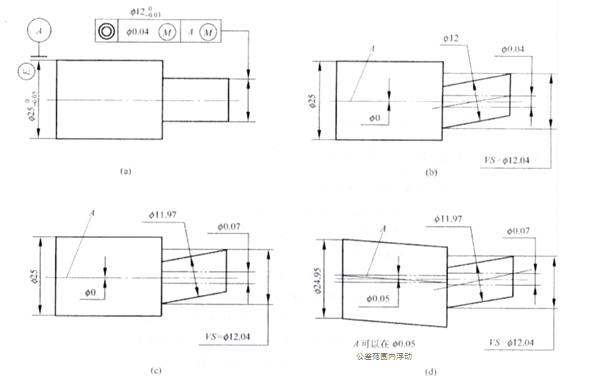
Kuvassa A on esitetty ulomman ympyrän akselin koaksiaalisuustoleranssi ulkokehän akseliin nähden. Mitatut elementit ja peruselementit täyttävät fyysiset maksimivaatimukset samanaikaisesti.
Kun elementti on suurimmassa kiinteässä tilassaan, sen akselin koaksiaalisuustoleranssi nollapisteeseen A on Ф0,04mm, kuten kuvassa B näkyy. Mitatun akselin tulee täyttää d fe≤Ф12.04mm, Ф11.97≤d al≤Ф12mm .
Kun pientä elementtiä mitataan, sen akselin koaksiaalisuusvirhe voi saavuttaa maksimiarvon. Tämä arvo on yhtä suuri kuin kahden toleranssin summa: piirustuksessa määritetty koaksiaalisuustoleranssi 0,04 mm ja akselin mittatoleranssi, joka on Ф0,07 mm (kuten kuvassa c).
Kun peruspisteen akseli on fyysisellä maksimirajalla, ulkokoon Ф25mm, annettu koaksiaalisuustoleranssi piirustuksessa voi olla Ф0.04mm. Jos peruspisteen ulkoinen koko pienenee fyysiseen vähimmäiskokoon Ф24,95 mm, peruspisteakseli voi kellua mittatoleranssin Ф0,05 mm sisällä. Kun akseli on äärimmäisessä kelluvassa tilassa, koaksiaalisuustoleranssi kasvaa nollapisteen mittatoleranssiarvoon Ф0,05 mm. Tämän seurauksena, kun mitattu ja peruselementti ovat samanaikaisesti minimikiintotilassa, suurin koaksiaalisuusvirhe voi olla jopa Ф0,12 mm (kuva d), mikä on 0,04 mm:n summa koaksiaalisuustoleranssille 0,03 mm. peruspisteen mittatoleranssille ja 0,05 mm peruspisteakselin kelluvalle toleranssille.
6. Kokonaisuuden vähimmäisvaatimukset ja niiden palautusvaatimukset
Jos näet piirustuksen geometrisessa toleranssilaatikossa toleranssiarvon tai peruspisteen kirjaimen perään merkittynä symbolikuvan, se tarkoittaa, että mitatun elementin tai peruspisteelementin on täytettävä vastaavasti fyysiset vähimmäisvaatimukset. Toisaalta, jos mitattavan elementin geometrisen toleranssiarvon jälkeen on symboli, se tarkoittaa, että käännettävää vaatimusta käytetään kokonaisuuden vähimmäisvaatimuksena.
1) Testin vaatimuksiin sovelletaan kokonaisuuden vähimmäisvaatimuksia
Kun mitattavalle elementille käytetään kokonaisuuden vähimmäisvaatimusta, elementin todellinen ääriviiva ei saa ylittää sen tehollista rajaa millään annetulla pituudella. Lisäksi elementin paikallinen todellinen koko ei saa ylittää sen enimmäis- tai vähimmäiskokoa.
Jos mitattuun ominaisuuteen sovelletaan kiintoaineen vähimmäisvaatimusta, geometrinen toleranssiarvo annetaan ominaisuuden ollessa vähimmäiskiinteässä tilassa. Kuitenkin, jos ominaisuuden todellinen ääriviiva poikkeaa sen pienimmästä kiinteästä koosta, muoto- ja sijaintivirhearvo voi ylittää alimmassa tilassa annetun toleranssiarvon. Tällaisissa tapauksissa mitatun kohteen aktiivinen koko ei saa ylittää sen kiinteää, tehollista rajakokoa.
2) Kokonaisuuden vähimmäisvaatimuksina käytetään palautuvia vaatimuksia
Kun käännettävää vaatimusta sovelletaan kiintoaineen vähimmäisvaatimukseen, mitatun ominaisuuden todellinen ääriviiva ei saa ylittää sen kiinteän, tehollisen vähimmäisrajaa millään annetulla pituudella. Lisäksi sen paikallinen todellinen koko ei saa ylittää suurinta kiinteää kokoa. Näissä olosuhteissa geometrinen virhe ei saa ylittää ainoastaan fyysisessä vähimmäistilassa annettua geometrista toleranssiarvoa, kun mitattavan elementin todellinen koko poikkeaa fyysisestä vähimmäiskoosta, vaan se saa myös ylittää fyysisen vähimmäiskoon, kun todellinen koko on erilainen, jos geometrinen virhe on pienempi kuin annettu geometrinen toleranssiarvo.
Thecnc koneistettuVähimmäismassaa ja sen käännettävyyttä koskevia vaatimuksia tulisi käyttää vain, kun geometristä toleranssia käytetään ohjaamaan liittyvää keskikohtaa. Kuitenkin, käytetäänkö näitä vaatimuksia vai ei, riippuu elementin erityisistä suorituskykyvaatimuksista.
Kun annettu geometrinen toleranssiarvo on nolla, suurimmat (minimi) kiintoainevaatimukset ja niiden palautuvat vaatimukset kutsutaan nollageometrisiksi toleransseiksi. Tässä vaiheessa vastaavat rajat muuttuvat, kun taas muut selitykset pysyvät ennallaan.
7. Geometristen toleranssiarvojen määrittäminen
1) Ruiskutusmuodon ja asennon toleranssiarvojen määrittäminen
Yleensä on suositeltavaa, että toleranssiarvot noudattavat tiettyä suhdetta siten, että muodon toleranssi on pienempi kuin sijaintitoleranssi ja mittatoleranssi. On kuitenkin tärkeää huomata, että epätavallisissa olosuhteissa hoikan akselin akselin suoruustoleranssi voi olla paljon suurempi kuin mittatoleranssi. Paikkatoleranssin tulee olla sama kuin mittatoleranssi ja se on usein verrattavissa symmetriatoleranssiin.
On tärkeää varmistaa, että paikannustoleranssi on aina suurempi kuin suuntatoleranssi. Paikannustoleranssi voi sisältää suuntatoleranssin vaatimukset, mutta päinvastoin ei pidä paikkaansa.
Lisäksi kokonaistoleranssin tulisi olla suurempi kuin yksittäisten toleranssien. Esimerkiksi sylinterin pinnan sylinterimäisyystoleranssi voi olla suurempi tai yhtä suuri kuin pyöreyden, perusviivan ja akselin suoruustoleranssi. Vastaavasti tason tasaisuustoleranssin tulisi olla suurempi tai yhtä suuri kuin tason suoruustoleranssi. Lopuksi kokonaisajon toleranssin tulisi olla suurempi kuin säteittäinen pyöreä juoksu, pyöreys, sylinterimäisyys, alkuviivan ja akselin suoruus ja vastaava koaksiaalisuustoleranssi.
2) Ilmoittamattomien geometristen toleranssiarvojen määrittäminen
Jotta tekniset piirustukset olisivat ytimekkäitä ja selkeitä, on valinnaista ilmoittaa piirustuksiin geometrinen toleranssi yleisessä työstökonetyöstössä helposti varmistettavan geometrisen tarkkuuden vuoksi. Elementeille, joiden muototoleranssivaatimuksia ei ole erikseen ilmoitettu piirustuksessa, vaaditaan myös muodon ja sijainnin tarkkuus. Katso GB/T 1184:n toteutusmääräykset. Piirustusesitykset ilman toleranssiarvoja tulee merkitä otsikkolohkon liitteeseen tai teknisiin vaatimuksiin ja teknisiin asiakirjoihin.
Laadukkaat auton varaosat,jyrsintäosat, jateräksestä sorvatut osatvalmistetaan Kiinassa, Anebonissa. Anebonin tuotteet ovat saaneet yhä enemmän tunnustusta ulkomaisilta asiakkailta ja luoneet heidän kanssaan pitkäaikaisia yhteistyösuhteita. Anebon tarjoaa parasta palvelua jokaiselle asiakkaalle ja toivottaa ystävät vilpittömästi tervetulleeksi työskentelemään Anebonin kanssa ja luomaan yhteisiä etuja yhdessä.
Postitusaika: 16.4.2024