E mohio ana te katoa ki te miro. Hei hoa mahi i roto i te umanga whakangao, he maha nga wa e hiahia ana matou ki te taapiri i nga miro kia rite ki nga hiahia o nga kaihoko i te wa e tukatuka ana i nga taputapu taputapu penei i teNga waahanga miihini CNC, Nga waahanga hurihuri CNCaNga waahanga mira CNC.
1. He aha te miro?
Ko te miro he helix kua tapahia ki tetahi mea mahi mai i waho, mai i roto ranei. Ko nga mahi matua o nga miro ko:
1. Hangaia he hononga miihini ma te whakakotahi i nga hua miro o roto me nga hua miro o waho.
2. Whakawhiti i te nekehanga ma te huri i te nekehanga hurihuri ki te nekehanga raina me te huri ke.
3. Tikina nga painga miihini.
2. Te kōtaha miro me ngā kupu
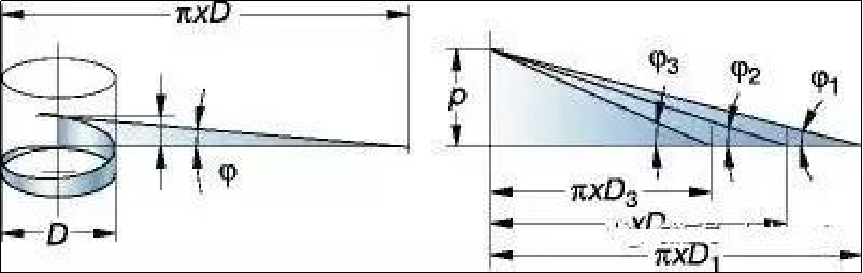
Ko te kōtaha miro e whakatau ana i te āhuahanga o te miro, tae atu ki te diameter o te mea mahi (nga taima nui, pitch, me te iti); koki kōtaha miro; ware me te koki helix.
1. Nga kupu miro
① Raro: Ko te mata o raro e hono ana i nga taha miro e rua.
② taha: te mata taha miro e hono ana i te tihi me te raro o te niho.
③Crest: Ko te mata o runga e hono ana i nga taha e rua.
P = pitch, mm, miro ranei mo ia inihi (tpi)
ß = koki kōtaha
ϕ = koki helix miro
d = te diameter nui o te miro o waho
D = te diameter nui o te miro o roto
d1 = iti te diameter o te miro o waho
D1 = He iti te diameter o te miro o roto
d2 = te diameter o te miro o waho
D2 = te diameter pitch miro o roto
Te diameter o te papa, d2/D2
Te diameter whai hua o te miro. Tata ki te haurua i waenga i nga diameter nui me te iti.
Ko te ahuahanga o te miro kei runga i te diameter pitch miro (d, D) me te pitch (P): te tawhiti axial i te taha o te miro i runga i te mea mahi mai i tetahi ira i runga i te whaarangi ki te waahi e whai ake nei. Ka kitea hoki tenei he tapatoru e hipa ana i te taonga mahi.
vc = tere tapahi (m/min)
ap = hohonu miro katoa (mm)
moe = hohonu miro katoa (mm)
tpi = miro mo ia inihi
Whangai = pitch
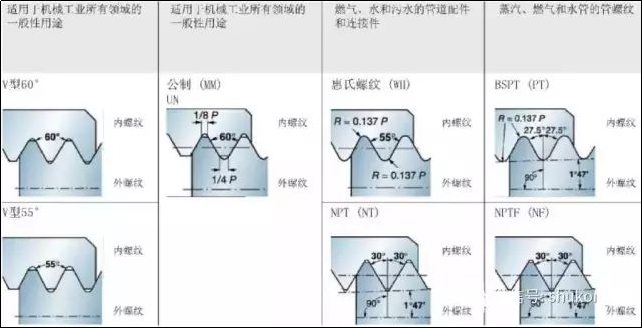
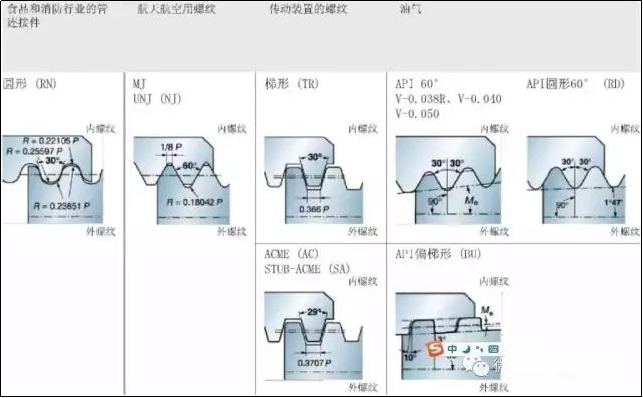
2. Kōtaha miro noa
1. Te tataunga me te manawanui o te diameter o te miro o waho o te 60° momo niho (paerewa motu GB197/196)
a. Te tātaitanga o te rahi taketake o te diameter pitch
Ko te rahi taketake o te diameter pitch o te miro = te diameter nui o te miro – pitch × uara whakarea.
Whakaaturanga tātai: d/DP×0.6495
2. Te tātaitanga me te aro o te diameter o te pitch o te miro o roto 60° (GB197/196)
a.6H taumata miro pitch diameter katakina (i runga i te miro pitch)
Tepe o runga:
P0.8+0.125P1.00+0.150P1.25+0.16P1.5+0.180
P1.25+0.00P2.0+0.212P2.5+0.224
Ko te uara tepe iti ko “0″,
Ko te tātai tātai tepe o runga 2+TD2 ko te rahi taketake + te manawanui.
Hei tauira, ko te diameter o te pitch o te miro o roto M8-6H: 7.188+0.160=7.348 Te rohe o runga: 7.188 te tepe o raro.
b. He rite tonu te tātai tātaitanga o te diameter pitch o te miro o roto ki te miro o waho
Arā, D2=DP×0.6495, arā, ko te diameter waenga o te miro o roto he rite ki te diameter nui o te uara taurite miro-pitch×.
c.6G karaehe miro pitch diameter taketake ine E1 (i runga i te miro pitch)
P0.8+0.024P1.00+0.026P1.25+0.028P1.5+0.032
P1.75+0.034P1.00+0.026P2.5+0.042
3. Te tataunga me te aro o te diameter nui o te miro o waho (GB197/196)
a. Ko te rohe o runga o te 6h te diameter nui o te miro o waho
Arā, ko te tauira uara diameter miro M8 ko te φ8.00 ko te “0″ te herenga o runga.
b. Te aro o te uara tepe iti o te diameter nui o te karaehe 6h o te miro o waho (i runga i te papa miro)
P0.8-0.15P1.00-0.18P1.25-0.212P1.5-0.236P1.75-0.265
P2.0-0.28P2.5-0.335
Te tātai tātai mo te tepe o raro o te diameter matua: d-Td te inenga taketake o te diameter nui o te miro – te manawanui.
4. Te tatauranga me te manawanui o te diameter iti o te miro o roto
a. Te tātaitanga o te rahi taketake o te diameter iti o te miro o roto (D1)
Te rahi taketake o te diameter iti o te miro = te rahi taketake o te miro o roto – te tauwehe pitch ×
5. Te tātai tātai o te wehenga upoko tikanga wehewehe kotahi
Te tātai tātai o te tikanga wehenga kotahi: n=40/Z
n: te maha o nga hurihanga me huri te upoko whakawehe
Z: He hautau rite o te mea mahi
40: te maha o te upoko wehewehe
6. Te tātai tātai o te hexagone kua tuhia ki te porowhita
① Kimihia te taha hexagonal te ritenga atu (S mata) o te porowhita D
S=0.866D ko te diameter×0.866 (te whakarea)
② Tātaihia te diameter o te porowhita (D) mai i nga taha o te taha o te hexagon (mata S)
Ko te D=1.1547S he taha anga whakamua×1.1547 (whakarea)
7. Te tātai tātai o ngā taha hexagonal me te hauroki i roto i te tukanga upoko makariri
① Kimihia te koki koki e mai i te taha (S) o te hauono o waho
e=1.13s he taha anga whakamua×1.13
②Kimihia te koki koki (e) mai i te taha o te taha o te hauono o roto
e=1.14s he taha anga whakamua×1.14 (whakarea)
③ Kimihia te diameter o te mahunga o te kokonga (D) mai i te taha (ng) o te taha ono o waho.
Ko te diameter o te porowhita (D) me tatau kia rite ki (te tauira tuarua i te 6) te taha hexagonal te ritenga atu (s mata), ka tika te whakanui ake i te uara o te pokapu, ara, D≥1.1547s. Ka taea anake te whakatau tata i te nui o te pokapu utu.
8. Te tātai tātai o te tapawhā kua tuhia ki te porowhita
① Porowhita (D) hei kimi i te taha o te taha o te tapawha (mata S)
S=0.7071D te diameter×0.7071
② Kimihia te porowhita (D) mai i nga taha o te tapawha (mata S)
Ko te D=1.414S kei te taha taha×1.414
9. Te tātai tātai o te tapawhā i te taha o te taha me te koki anga whakamua i roto i te tukanga upoko makariri
① Kimihia te koki koki (e) mai i te taha (S) o te tapawha o waho
Ko te e=1.4s te taha o te taha (s)×1.4 tawhā
② Kimihia te koki koki (e) mai i te taha o te taha o te tapawha o roto
Ko te e=1.45s te taha o te taha (s)×1.45 whakarea
10. Te tātai mō te tātai i te rōrahi o te hexagon
s20.866×H/m/k te tikanga o te taha ritenga×te ritenga o te taha×0.866×te teitei, te matotoru ranei.
11. Te tātai tātai o te rōrahi o te tinana frustum (koe).
Ko te 0.262H(D2+d2+D×d) he 0.262×te teitei×(te whanui o te upoko nui×te diameter o te upoko nui+te diameter o te mahunga iti×te diameter o te mahunga iti+te diameter o te upoko nui×te diameter o te upoko iti).
12. Tātai tātai mō te rōrahi o te tinana porowhita (pērā i te pane hauwhā porohita)
Ko te 3.1416h2(Rh/3) he 3.1416×te teitei×te teitei×(radius-teitei÷3).
13. Te tātai tātai mō te hanga i ngā rahinga o ngā kōrere mō ngā miro o roto
1. Te tataunga o te tap nui te diameter D0
D0=D+(0.866025P/8)×(0.5~1.3) Ko te rahi taketake o te miro diameter nui tap + 0.866025 pitch ÷ 8×0.5 ki te 1.3.
Tuhipoka: Ko te whiriwhiri o te 0.5 ki te 1.3 me whakapumau i runga i te rahi o te pitch. Ko te nui o te uara pitch, me whakamahi te whakarea iti. Engari, ko te iti ake o te uara pitch, me whakamahi te whakarea nui ake.
2. Te tātaitanga o te diameter tap pitch (D2)
D2=(3×0.866025P)/8, ara, tap diameter=3×0.866025×pitch÷8
3. Te tātai i te diameter tap (D1)
D1=(5×0.866025P)/8 ko te tap diameter=5×0.866025×pitch÷8
14. Te tātai tātai mō te roa o ngā rawa e whakamahia ana mō te hanga pane makariri ki ngā momo āhua
E mōhiotia ana ko te tātai rōrahi o te porowhita he diameter×diameter×0.7854×roa, radius×radius×3.1416×roa. Arā, d2×0.7854×L or R2×3.1416×L
Ina tātaihia, ko te rōrahi X÷diameter÷diameter÷0.7854 or X÷radius÷radius÷3.1416 o te rauemi e hiahiatia ana mo te tukatukanga waahanga miihini cncanga waahanga hurihuri cncko te roa o te rauemi.
Tātai tīwae = X/(3.1416R2) X/0.7854d2 rānei
Ko te X kei te tauira e tohu ana i te uara rōrahi o te rauemi e hiahiatia ana;
Ko te L e tohu ana i te uara roa o te kai tuturu;
Ko te R/d e tohu ana i te radius, te diameter ranei o te whangai.
Wā tuku: Hānuere-11-2023